题目内容
16.已知函数$f(x)={x}^{2}+2xsinθ-1,x∈[-\frac{\sqrt{3}}{2},\frac{1}{2}]$.(1)若$θ=\frac{π}{6}$,若f(x)<m恒成立,求实数m的范围;
(2)若f(x)在x∈[-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$]上是单调函数,且θ∈[0,2π),求θ的取值范围.
分析 (1)θ=$\frac{π}{6}$时,f(x)=x2+x-1,f′(x)=2x+1,由此利用导数性质能求出函数的最值.
(2)f(x)=x2+2xsinθ-1的图象的对称轴为x=-sinθ,由于f(x)在x∈[-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$]上是单调增函数,得-sinθ≤-$\frac{\sqrt{3}}{2}$,由此能求出θ的取值范围
解答 解:(1)∵θ=$\frac{π}{6}$,函数f(x)=x2+2xsinθ-1,x∈[-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$].
∴f(x)=x2+x-1,f′(x)=2x+1,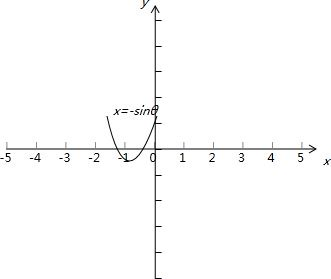
由f′(x)=0,得x=-$\frac{1}{2}$,
∴函数f(x)在[-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$)递减,在(-$\frac{1}{2}$,$\frac{1}{2}$]递增,
∴f(x)最大值=f(-$\frac{\sqrt{3}}{2}$),或f($\frac{1}{2}$),
f($\frac{1}{2}$)=$\frac{1}{4}$+$\frac{1}{2}$-1=-$\frac{1}{4}$<f(-$\frac{\sqrt{3}}{2}$)=$\frac{3}{4}$+$\frac{\sqrt{3}}{2}$-1=$\frac{\sqrt{3}}{2}$-$\frac{1}{4}$
∴x=-$\frac{\sqrt{3}}{2}$时,f(x)的最大值为$\frac{\sqrt{3}}{2}$-$\frac{1}{4}$,
∴m>$\frac{\sqrt{3}}{2}$-$\frac{1}{4}$;
(2)f(x)=x2+2xsinθ-1的图象的对称轴为x=-sinθ,
θ∈[0,2π),-sinθ<0,
由于f(x)在x∈[-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$]上是单调函数,
所以-sinθ≤-$\frac{\sqrt{3}}{2}$,
即sinθ≥$\frac{\sqrt{3}}{2}$,又∵θ∈[0,2π)
所求θ的取值范围是[$\frac{π}{3}$,$\frac{2π}{3}$].
点评 本题考查函数的最值的求法,考查角的取值范围的求法,解题时要认真审题,注意导数性质和三角函数知识的合理运用.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
| A. | 42 | B. | 40 | C. | 36 | D. | 53 |
 将非零自然数列按一定的规则排成如图所示的三角形数列表(每一行比上一行多一个数),设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,如a42=8,若aij=2014则i,j的值分别为( )
将非零自然数列按一定的规则排成如图所示的三角形数列表(每一行比上一行多一个数),设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,如a42=8,若aij=2014则i,j的值分别为( )| A. | i=62,j=15 | B. | i=62,j=14 | C. | i=64,j=14 | D. | i=64,j=15 |
| A. | ($\frac{1}{2},2$] | B. | (1,3] | C. | (2,3] | D. | [3,5] |