题目内容
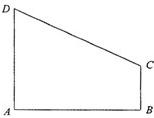 如图,直角梯形ABCD中∠DAB=90°,AD∥BC,AB=2,AD=
如图,直角梯形ABCD中∠DAB=90°,AD∥BC,AB=2,AD=| 3 |
| 2 |
| 1 |
| 2 |
(Ⅰ)建立适当坐标系,求椭圆G的方程;
(Ⅱ)若点E满足
| EC |
| 1 |
| 2 |
| AB |
分析:(1)先以AB所在直线为x轴,AB中垂线为y轴建立直角坐标系,进而可知A,B的坐标,设椭圆的标准方程,根据AB的距离求得c,把x=c代入椭圆方程,求得
=
,进而根据a,b和c的关系求得a和b,则椭圆的方程可得.
(2)设出直线l的方程,代入椭圆方程消去y,根据判别式得出k和m的不等式关系,设M,N和MN中点的坐标,进而根据韦达定理得出x0和y0的表达式,进而根据|ME|=|NE|,可推断出MN⊥EF,进而表示出两直线的斜率使其乘积等于-1求得m和k的关系,进而根据m和k的不等式关系确定k的范围.
| b2 |
| a |
| 3 |
| 2 |
(2)设出直线l的方程,代入椭圆方程消去y,根据判别式得出k和m的不等式关系,设M,N和MN中点的坐标,进而根据韦达定理得出x0和y0的表达式,进而根据|ME|=|NE|,可推断出MN⊥EF,进而表示出两直线的斜率使其乘积等于-1求得m和k的关系,进而根据m和k的不等式关系确定k的范围.
解答: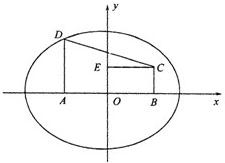 解:(Ⅰ)如图,以AB所在直线为x轴,
解:(Ⅰ)如图,以AB所在直线为x轴,
AB中垂线为y轴建立直角坐标系,?A(-1,0),B(1,0).
设椭圆方程为
+
=1.
令x=c?y0=
,
∴
?
.
∴椭圆C的方程是:
+
=1;
(Ⅱ)
=
?E(0,
),l⊥AB时不符;
设l:y=kx+m(k≠0),
由
?(3+4k2)x2+8kmx+4m2-12=0.
M、N存在??△>0?64k2m2-4(3+4k2)•(4m2-12)>0?4k2+3≥m2.
设M(x1,y1),N(x2,y2),MN的中点F(x0,y0)
∴x0=
=-
,
y0=kx0+m=
.
|ME|=|NE|?MN⊥EF?
=-
?
=-
?m=-
,
∴4k2+3≥(-
)2,∴4k2+3≤4,
∴0<k2≤1,∴-1≤k≤1且k≠0.
∴l与AB的夹角的范围是(0,
].
 解:(Ⅰ)如图,以AB所在直线为x轴,
解:(Ⅰ)如图,以AB所在直线为x轴,AB中垂线为y轴建立直角坐标系,?A(-1,0),B(1,0).
设椭圆方程为
| x2 |
| a2 |
| y2 |
| b2 |
令x=c?y0=
| b2 |
| a |
∴
|
|
∴椭圆C的方程是:
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)
| EC |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
设l:y=kx+m(k≠0),
由
|
M、N存在??△>0?64k2m2-4(3+4k2)•(4m2-12)>0?4k2+3≥m2.
设M(x1,y1),N(x2,y2),MN的中点F(x0,y0)
∴x0=
| x1+x2 |
| 2 |
| 4km |
| 3+4k2 |
y0=kx0+m=
| 3m |
| 3+4k2 |
|ME|=|NE|?MN⊥EF?
y0-
| ||
| x0 |
| 1 |
| k |
| ||||
-
|
| 1 |
| k |
| 3+4k2 |
| 2 |
∴4k2+3≥(-
| 3+4k2 |
| 2 |
∴0<k2≤1,∴-1≤k≤1且k≠0.
∴l与AB的夹角的范围是(0,
| π |
| 4 |
点评:本题主要考查了椭圆的标准方程和直线与椭圆的关系.考查了学生转化和化归的数学思想,基本的运算能力.

练习册系列答案
相关题目
 (2014•宜宾一模)如图,直角梯形ABCD中,∠ABC=∠BAD=90°,AB=BC且△ABC的面积等于△ADC面积的
(2014•宜宾一模)如图,直角梯形ABCD中,∠ABC=∠BAD=90°,AB=BC且△ABC的面积等于△ADC面积的 (2013•惠州一模)如图,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2
(2013•惠州一模)如图,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2

 .梯形ABCD所在平面外有一点P,满足PA⊥平面ABCD,PA=PB.
.梯形ABCD所在平面外有一点P,满足PA⊥平面ABCD,PA=PB.