题目内容
3.实数a,b,c,d满足|b-a+2|+(c+d2-3lnd)2=0,则(b-d)2+(a-c)2的最小值是8.分析 化简可得a=b+2,c=3lnd-d2,从而可得点(b,a)在函数f(x)=x+2的图象上,点(d,c)在函数g(x)=3lnx-x2的图象上;从而问题化为求函数g(x)=3lnx-x2上的点到直线f(x)=x+2的距离的最小值;结合图象求解即可.
解答 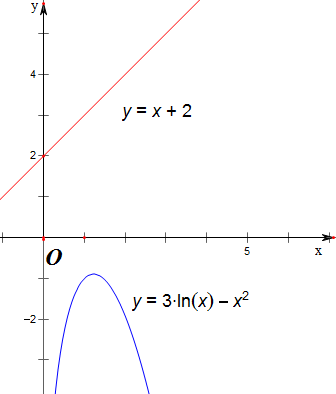 解:由题意可知,
解:由题意可知,
b-a+2=0,c+d2-3lnd=0;
故a=b+2,c=3lnd-d2,
即点(b,a)在函数f(x)=x+2的图象上,
点(d,c)在函数g(x)=3lnx-x2的图象上,
故求(b-d)2+(a-c)2的最小值可转化为
求函数g(x)=3lnx-x2上的点到直线f(x)=x+2的距离的最小值;
令g′(x)=$\frac{3}{x}$-2x=1得,x=1;
故点(1,-1)到直线f(x)=x+2的距离最小,
d=$\frac{|1+2-(-1)|}{\sqrt{1+1}}$=2$\sqrt{2}$;
故(b-d)2+(a-c)2的最小值是$(2\sqrt{2})^{2}$=8;
故答案为:8.
点评 本题考查了导数的综合应用及几何意义的应用,将问题转化为求函数g(x)=3lnx-x2上的点到直线f(x)=x+2的距离的最小值是个难点,属于难题.

练习册系列答案
相关题目
18.复数$\frac{\sqrt{2}+i}{1-\sqrt{2}i}$=( )
| A. | i | B. | -i | C. | 2($\sqrt{2}$+i) | D. | 1+i |
8.已知log${\;}_{\frac{1}{2}}$a<log${\;}_{\frac{1}{2}}$b,则下列不等式一定成立的是( )
| A. | ${(\frac{1}{4})^a}<{(\frac{1}{4})^b}$ | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ln(a-b)>0 | D. | 3a-b<1 |
15. 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则零件的体积与原来毛坯体积的比值为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则零件的体积与原来毛坯体积的比值为( )
 如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则零件的体积与原来毛坯体积的比值为( )
如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则零件的体积与原来毛坯体积的比值为( )| A. | $\frac{10}{27}$ | B. | $\frac{17}{27}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{9}$ |
15.抛物线x2=-$\frac{1}{4}$y的焦点坐标为( )
| A. | (-$\frac{1}{8}$,0) | B. | (0,-$\frac{1}{8}$) | C. | (0,-$\frac{1}{16}$) | D. | (-$\frac{1}{16}$,0) |
 底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{{4\sqrt{2}}}{3}$,则该半球的体积为$\frac{4\sqrt{2}π}{3}$.
底面是正多边形,顶点在底面的射影是底面中心的棱锥叫正棱锥.如图,半球内有一内接正四棱锥S-ABCD,该四棱锥的体积为$\frac{{4\sqrt{2}}}{3}$,则该半球的体积为$\frac{4\sqrt{2}π}{3}$.
 已知抛物线的顶点在原点,焦点F在x轴上,且抛物线上横坐标为1的点到F的距离为2,过点F的直线交抛物线于A,B两点.
已知抛物线的顶点在原点,焦点F在x轴上,且抛物线上横坐标为1的点到F的距离为2,过点F的直线交抛物线于A,B两点.