题目内容
为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图(如右图),已知从左到右各长方形高的比为2:3:5:6:3:1,则该班学生数学成绩在(80,100)之间的学生人数是
 . 32人
. 32人  . 27人
. 27人  . 24人
. 24人  . 33人
. 33人
 . 32人
. 32人  . 27人
. 27人  . 24人
. 24人  . 33人
. 33人
D
根据题意可得该办六个分数段的概率比例依次为2:3:5:6:3:1,进而得到成绩在(80,90)与(90,100)之间的学生人数的概率,即可得到答案.
解:由题意可得:从左到右各长方形高的比为2:3:5:6:3:1,
所以(60,70),(70,80),(80,90),(90,100),(100,110),(110,120)各分数段的概率之比为2:3:5:6:3:1,
所以该班学生数学成绩在(80,90)与(90,100)之间的学生人数的概率分别为: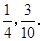
所以该班学生数学成绩在(80,100)之间的学生人数是:60×(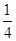 +
+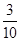 )=33.
)=33.
故选D.
解:由题意可得:从左到右各长方形高的比为2:3:5:6:3:1,
所以(60,70),(70,80),(80,90),(90,100),(100,110),(110,120)各分数段的概率之比为2:3:5:6:3:1,
所以该班学生数学成绩在(80,90)与(90,100)之间的学生人数的概率分别为:
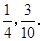
所以该班学生数学成绩在(80,100)之间的学生人数是:60×(
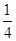 +
+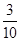 )=33.
)=33.故选D.

练习册系列答案
相关题目
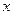
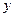
 个人,其中35岁以
个人,其中35岁以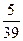 ,求
,求 交的作品的件数按5天一组分组统计,绘制了频率分布直方图,如图所示,已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为 12 ,请解答下列问题:
交的作品的件数按5天一组分组统计,绘制了频率分布直方图,如图所示,已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为 12 ,请解答下列问题: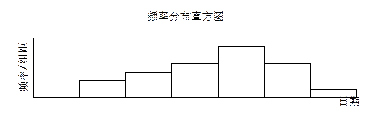
 与
与 之间的数据如下表所示,
之间的数据如下表所示,




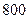 名学生中随机抽取
名学生中随机抽取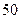 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于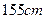 和
和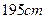 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组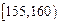 .第二组
.第二组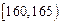 ;…第八组
;…第八组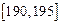 ,右图
,右图


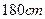 以上(含
以上(含 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有 ,
, 之间的一组数据:
之间的一组数据: 必过点
必过点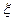 的概率分布律如下表:
的概率分布律如下表: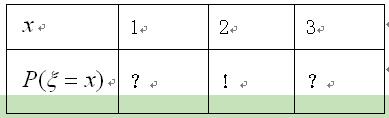
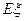 = .
= .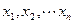 的方差是2, 则样本
的方差是2, 则样本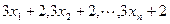 的方差是 _____________
的方差是 _____________