题目内容
2. 如图,已知四边形ABCD内接于半径为3的圆,且AB是圆的直径,过点D的圆的切线与BA的延长线交于点M,∠BMD的平分线分别交AD、BD于点E、F,AC、BD交于点P.
如图,已知四边形ABCD内接于半径为3的圆,且AB是圆的直径,过点D的圆的切线与BA的延长线交于点M,∠BMD的平分线分别交AD、BD于点E、F,AC、BD交于点P.(Ⅰ)证明:DE=DF;
(Ⅱ)若DM=3$\sqrt{3}$,AP=2CP=2$\sqrt{3}$,求BP的长.
分析 (Ⅰ)证明:DE=DF,只要证明∠DEF=∠DFE;
(Ⅱ)先求出∠ABD=30°,BD=ABcos∠ABD=3$\sqrt{3}$,再利用相交弦定理,即可求BP的长.
解答 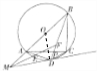 (Ⅰ)证明:∵MD是切线,AD是弦,
(Ⅰ)证明:∵MD是切线,AD是弦,
∴∠ADM=∠ABD,
∵∠BMF=∠DMF,
∴∠BMF+∠ABD=∠ADM+∠DMF,
∵∠DEF=∠ADM+∠DMF,∠DFE=∠BMF+∠ABD,
∴∠DEF=∠DFE,
∴DE=DF;
(Ⅱ)解:连接OD,则
∵MD是切线,
∴OD⊥MD,
∵OD=3,MD=3$\sqrt{3}$,
∴∠MOD=60°,∴∠ABD=30°,
Rt△ABD中,AB=6,∴BD=ABcos∠ABD=3$\sqrt{3}$,
∵四边形ABCD内接于圆O,
∴AP•PC=BP•PD,
∴2$\sqrt{3}×\sqrt{3}$=BP•(3$\sqrt{3}$-BP),
∴BP=$\sqrt{3}$或2$\sqrt{3}$,
∵BP>CP,∴BP=2$\sqrt{3}$.
点评 本题考查圆的切线的性质,考查相交弦定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
10.微信是现代生活进行信息交流的重要工具,距据统计,某公司200名员工中90%的人使用微信,其中每天使用微信时间在一小时以内的有60人,其余每天使用微信在一小时以上,若将员工年龄分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,使用微信的人中75%是青年人,若规定:每天使用微信时间在一小时以上为经常使用微信,经常使用微信的员工中$\frac{2}{3}$是青年人.
(Ⅰ)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出2×2列联表.
2×2列联表.
(Ⅱ)由列联表中所得数据,是否有99.9%的把握认为“经常使用微信与年龄有关”?
(Ⅲ)采用分层抽样的方法从“经常使用微信”中抽取6人,从这6人中任选2人,求事件A“选出的2人均是青年人”的概率.
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
(Ⅰ)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出2×2列联表.
2×2列联表.
| 青年人 | 中年人 | 合计 | |
| 经常使用微信 | |||
| 不经常使用微信 | |||
| 合计 |
(Ⅲ)采用分层抽样的方法从“经常使用微信”中抽取6人,从这6人中任选2人,求事件A“选出的2人均是青年人”的概率.
附:
| P(K2≥k) | 0.010 | 0.001 |
| k | 6.635 | 10.828 |
17.已知集合A={x|1<x<4},B={x|x≤2},则A∩(∁RB)等于( )
| A. | (1,2] | B. | [2,4) | C. | (2,4) | D. | (1,4) |

 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC的中点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$. 如图,已知椭圆:$\frac{{x}^{2}}{4}$+y2=1,点A,B是它的两个顶点,过原点且斜率为k的直线l与线段AB相交于点D,且与椭圆相交于E、F两点.
如图,已知椭圆:$\frac{{x}^{2}}{4}$+y2=1,点A,B是它的两个顶点,过原点且斜率为k的直线l与线段AB相交于点D,且与椭圆相交于E、F两点. 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°PA=PD=AD=2BC=2,CD=$\sqrt{3},PB=\sqrt{6}$,Q是AD的中点,M是棱PC上的点,且PM=3MC.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°PA=PD=AD=2BC=2,CD=$\sqrt{3},PB=\sqrt{6}$,Q是AD的中点,M是棱PC上的点,且PM=3MC.