题目内容
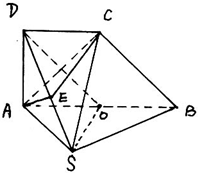 (2012•芜湖二模)如图,四棱锥S-ABCD的底面ABCD是直角梯形,侧面SAB是等边三角形,DA⊥面SAB,DC∥AB,AB=2AD=2DC,O,E分别为AB、SD中点.
(2012•芜湖二模)如图,四棱锥S-ABCD的底面ABCD是直角梯形,侧面SAB是等边三角形,DA⊥面SAB,DC∥AB,AB=2AD=2DC,O,E分别为AB、SD中点.(1)求证:SO∥面AEC,BC⊥面AEC
(2)求二面角O-SD-B的余弦值.
分析:(1)设DO,AC交于点F,连接EF,易判断AOCD为正方形,进而AC与BC垂直平分,结合已知及三角形中位线定理可得EF∥OS,进而由线面平行的判定定理得到SO∥面AEC;根据已知可先证得SO⊥面ABCD,进而得到SO⊥BC,而由BC与OD平行与AC垂直,结合线面垂直的判定定理可得BC⊥面AEC
(2)分别以OS,OB,OC为x轴,Y轴,z轴点的空间直角坐标系,设AB=2,分别求出二面角O-SD-B的两个半平面的法向量,代入向量夹角公式,可得答案.
(2)分别以OS,OB,OC为x轴,Y轴,z轴点的空间直角坐标系,设AB=2,分别求出二面角O-SD-B的两个半平面的法向量,代入向量夹角公式,可得答案.
解答:证明:(1)设DO,AC交于点F,连接EF,
∵直角梯形ABCD中,AB=2AD=2DC,
故四边形AOCD为正方形,则F为DO中点
∵E为DS的中点
∴在△DOS中EF∥OS
又∵EF?面AEC,OS?面AEC
∴SO∥面AEC…(3分)
∵DA⊥面SAB,SO?面SAB
∴DA⊥SO,
又∵侧面SAB是等边三角形,O为AB的中点,
∴AB⊥SO,∵AB∩DA=A
∴SO⊥面ABCD
又∵BC?面ABCD
∴SO⊥BC,EF⊥BC
又BC∥DO
∴BC⊥AC,∵EF∩AC=F
∴BC⊥面AEC…(6分)
(2)分别以OS,OB,OC为x轴,Y轴,z轴点的空间直角坐标系,
设AB=2,显然AC⊥面SOD,
∴面SOD的法向量
=
=(0,1.1)
设面SBD 的法向量为
=(1,x,y)
由
⊥
,
⊥
求得:
=(1,
,2
)是面SBD的一个法向量,
∴cosθ=
=
=
故所求二面角的余弦值为
…(12分)
∵直角梯形ABCD中,AB=2AD=2DC,
故四边形AOCD为正方形,则F为DO中点
∵E为DS的中点
∴在△DOS中EF∥OS
又∵EF?面AEC,OS?面AEC
∴SO∥面AEC…(3分)
∵DA⊥面SAB,SO?面SAB
∴DA⊥SO,
又∵侧面SAB是等边三角形,O为AB的中点,
∴AB⊥SO,∵AB∩DA=A
∴SO⊥面ABCD
又∵BC?面ABCD
∴SO⊥BC,EF⊥BC
又BC∥DO
∴BC⊥AC,∵EF∩AC=F
∴BC⊥面AEC…(6分)
(2)分别以OS,OB,OC为x轴,Y轴,z轴点的空间直角坐标系,
设AB=2,显然AC⊥面SOD,
∴面SOD的法向量
| m |
| AC |
设面SBD 的法向量为
| n |
由
| n |
| SB |
| n |
| SD |
求得:
| n |
| 3 |
| 3 |
∴cosθ=
| ||||
|
|
3
| ||
|
| 3 |
| 8 |
| 6 |
故所求二面角的余弦值为
| 3 |
| 8 |
| 6 |
点评:本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定,二面角的平面角,(1)的关键是熟练掌握空间线面关系的判定定理及性质定理,能熟练的进行转化,(2)的关键是构造空间坐标系,将二面角转化为向量夹角.

练习册系列答案
相关题目
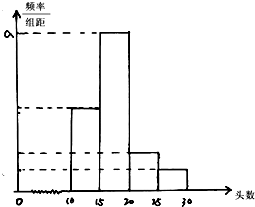 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: