题目内容
如图，设E：
＝1(a＞b＞0)的焦点为F1与F2，且P∈E，∠F1PF2＝2θ.求证：△PF1F2的面积S＝b2tanθ.
＝1(a＞b＞0)的焦点为F1与F2，且P∈E，∠F1PF2＝2θ.求证：△PF1F2的面积S＝b2tanθ.见解析
设|PF1|＝r1，|PF2|＝r2，则S＝
r1r2sin2θ.又|F1F2|＝2c，
由余弦定理有(2c)2＝
＋
－2r1r2cos2θ＝(r1＋r2)2－2r1r2－2r1r2cos2θ＝(2a)2－2r1r2(1＋cos2θ)，于是2r1r2(1＋cos2θ)＝4a2－4c2＝4b2.
所以r1r2＝
.这样即有S＝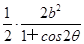
sin2θ＝b2
＝b2tanθ.
r1r2sin2θ.又|F1F2|＝2c，由余弦定理有(2c)2＝
＋－2r1r2cos2θ＝(r1＋r2)2－2r1r2－2r1r2cos2θ＝(2a)2－2r1r2(1＋cos2θ)，于是2r1r2(1＋cos2θ)＝4a2－4c2＝4b2.所以r1r2＝
.这样即有S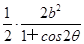＝sin2θ＝b2＝b2tanθ.
练习册系列答案
阅读快车系列答案
相关题目
与抛物线
的焦点重合，过
与椭圆相交于不同两点A和B，且满足
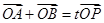（O为坐标原点），求实数t的取值范围.
＝1的顶点，过坐标原点的直线交椭圆于P、A两点，其中P在第一象限，过P作x轴的垂线，垂足为C，连结AC，并延长交椭圆于点B，设直线PA的斜率为k.
，它的一个顶点恰好是抛物线
的焦点．
APQ=
，且它的四条边与坐标轴平行，正方形GHPQ的顶点G,H在椭圆上，顶点P，Q在正方形的边EF上．且CD=2PQ=
．
，圆
，过椭圆上任一与顶点不重合的点P引圆O的两条切线，切点分别为A,B，直线AB与x轴,y轴分别交于点M,N，则
_____________
＋y2＝1(a＞1)的上顶点为M(0，1)，两条过M的动弦MA、MB满足MA⊥MB.
，求a；
＝1(a＞b＞0)的离心率为
，其左焦点到点P(2，1)的距离为
.不过原点O的直线l与C相交于A，B两点，且线段AB被直线OP平分．
＝1(a>b>0)的左、右焦点，A，B分别是椭圆E的左、右顶点，且
＋5
＝0.