题目内容
【题目】四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,侧面PAD⊥底面ABCD,∠BCD=60°,PA=PD= ![]() ,E是BC中点,点Q在侧棱PC上.
,E是BC中点,点Q在侧棱PC上. 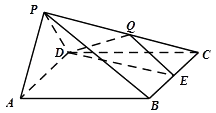
(1)求证:AD⊥PB;
(2)若Q是PC中点,求二面角E﹣DQ﹣C的余弦值;
(3)若 ![]() ,当PA∥平面DEQ时,求λ的值.
,当PA∥平面DEQ时,求λ的值.
【答案】
(1)证明:取AD中点O,连接OP,OB,BD.
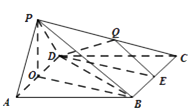
因为PA=PD,所以PO⊥AD.
因为菱形ABCD中,∠BCD=60°,所以AB=BD,所以BO⊥AD.
因为BO∩PO=O,所以AD⊥平面POB,所以AD⊥PB.
(2)解:由(1)知BO⊥AD,PO⊥AD.
因为侧面PAD⊥底面ABCD,且平面PAD∩底面ABCD=AD,所以PO⊥底面ABCD.
以O为坐标原点,如图建立空间直角坐标系O﹣xyz.
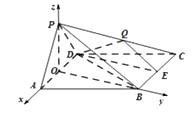
则D(﹣1,0,0), ![]() ,P(0,0,1),
,P(0,0,1), ![]() ,
,
因为Q为PC中点,所以 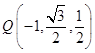 .
.
所以 ![]() ,
, 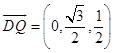 ,所以平面DEQ的法向量为
,所以平面DEQ的法向量为 ![]() .
.
因为 ![]() ,
, 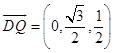 ,
,
设平面DQC的法向量为 ![]() ,则
,则  ,∴
,∴ 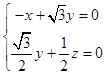
令 ![]() ,则y=1,
,则y=1, ![]() ,即
,即 ![]() .
. 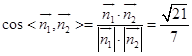 .
.
由图可知,二面角E﹣DQ﹣C为锐角,所以余弦值为 ![]() .
.
(3)解:因为 ![]() ,所以
,所以 ![]() ,
,
由(2)知 ![]() ,
, ![]() ,
,
若设Q(x,y,z),则 ![]() ,
,
由 ![]() ,得
,得 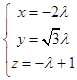 ,
,
在平面DEQ中, ![]() ,
, ![]() ,
,
所以平面DEQ法向量为 ![]() ,
,
又因为PA∥平面DEQ,所以 ![]() ,
,
即(1﹣λ)+(﹣1)(2λ﹣1)=0,得 ![]() .
.
所以,当 ![]() 时,PA∥平面DEQ.
时,PA∥平面DEQ.
【解析】(1)证明AD⊥平面POB,即可证明AD⊥PB;(2)证明PO⊥底面ABCD,建立空间直角坐标系,求出平面DEQ的法向量为 ![]() ,平面DQC的法向量
,平面DQC的法向量 ![]() ,利用向量的夹角公式,即可求得结论;(3)求出平面DEQ法向量为
,利用向量的夹角公式,即可求得结论;(3)求出平面DEQ法向量为 ![]() ,利用PA∥平面DEQ,即
,利用PA∥平面DEQ,即 ![]() ,从而可得结论.
,从而可得结论.
【考点精析】通过灵活运用直线与平面平行的判定和直线与平面垂直的性质,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;垂直于同一个平面的两条直线平行即可以解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某市政府为了实施政府绩效管理、创新政府公共服务模式、提高公共服务效率.实施了“政府承诺,等你打分”民意调查活动,通过问卷调查了学生、在职人员、退休人员共250人,统计结果表不幸被污损,如表:
学生 | 在职人员 | 退休人员 | |
满意 |
|
| 78 |
不满意 | 5 |
| 12 |
若在所调查人员中随机抽取1人,恰好抽到学生的概率为0.32.
(1)求满意学生的人数;
(2)现用分层抽样的方法在所调查的人员中抽取25人,则在职人员应抽取多少人?
(3)若满意的在职人员为77,则从问卷调查中填写不满意的“学生和在职人员”中选出2人进行访谈,求这2人中包含了两类人员的概率.