题目内容
已知函数f(x)=ax3-3x2+1-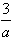 ,
,
(Ⅰ)若函数f(x)在x=-1时取到极值,求实数a的值;
(Ⅱ)试讨论函数f(x)的单调性;
(Ⅲ)当a>1时,在曲线y=f(x)上是否存在这样的两点A,B,使得在点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,若存在,试求a的取值范围;若不存在,请说明理由。
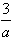 ,
,(Ⅰ)若函数f(x)在x=-1时取到极值,求实数a的值;
(Ⅱ)试讨论函数f(x)的单调性;
(Ⅲ)当a>1时,在曲线y=f(x)上是否存在这样的两点A,B,使得在点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,若存在,试求a的取值范围;若不存在,请说明理由。
解: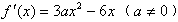 ,
,
(Ⅰ)∵函数f(x)在x=-1时取到极值,
∴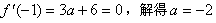 ,
,
经检验a=-2函数f(x)在x=-1时取到极小值,
∴实数a的值-2;
(Ⅱ)由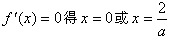 ,
,
①当 ,由
,由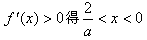 ,
,
由 ,
,
∴函数f(x)的单调增区间为 ,单调减区间为
,单调减区间为 ;
;
②当 ,
,
同理可得函数f(x)的单调增区间为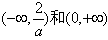 ,单调减区间为
,单调减区间为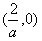 。
。
(Ⅲ)假设存在满足要求的两点A,B,即在点A、B处的切线都与y轴垂直,则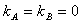 ,
,
即 ,
,
∴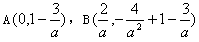 ,
,
又线段AB与x轴有公共点,
∴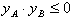 ,
,
即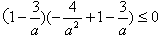 ,
,
又a>1,
解得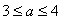 ,
,
所以当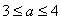 时,存在满足要求的点A、B。
时,存在满足要求的点A、B。
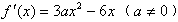 ,
,(Ⅰ)∵函数f(x)在x=-1时取到极值,
∴
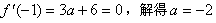 ,
,经检验a=-2函数f(x)在x=-1时取到极小值,
∴实数a的值-2;
(Ⅱ)由
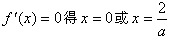 ,
,①当
 ,由
,由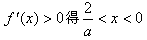 ,
,由
 ,
,∴函数f(x)的单调增区间为
 ,单调减区间为
,单调减区间为 ;
;②当
 ,
,同理可得函数f(x)的单调增区间为
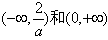 ,单调减区间为
,单调减区间为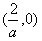 。
。(Ⅲ)假设存在满足要求的两点A,B,即在点A、B处的切线都与y轴垂直,则
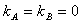 ,
,即
 ,
,∴
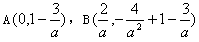 ,
,又线段AB与x轴有公共点,
∴
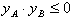 ,
,即
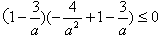 ,
,又a>1,
解得
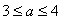 ,
,所以当
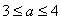 时,存在满足要求的点A、B。
时,存在满足要求的点A、B。
练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目