题目内容
(本小题满分12分)
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
【答案】
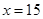 时,f(x)取最小值
时,f(x)取最小值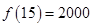 元;
元;
【解析】
试题分析:解本小题的关键是设楼房每平方米的平均综合费为f(x)元后,求得
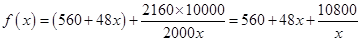
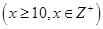 ,
,
然后利用导数研究其最值即可.
设楼房每平方米的平均综合费为f(x)元,则
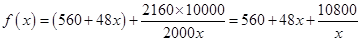
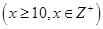
---- 4分
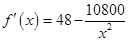 ,
令
,
令 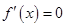 得
得 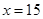 ---------
8分
---------
8分
当 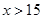 时,
时,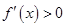 ;当 1
;当 1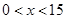 时,
时,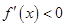 ---------10分
---------10分
因此 当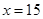 时,f(x)取最小值
时,f(x)取最小值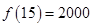 元;
----- 12分
元;
----- 12分
考点:导数在实际问题当中的应用.
点评:利用导数研究最优的实际问题,要先建立函数模型,然后再利用导数研究其极值即可.高考利用导数研究的应用题,一般都是单峰函数,函数的最值在极值取得.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目