题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,现将
的中点,现将![]() 与
与![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
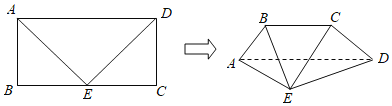
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析 (2)二面角![]() 的平面角余弦值为
的平面角余弦值为![]() .
.
【解析】
(1)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,证明
,证明![]() 即可;
即可;
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,求出平面
,求出平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,计算
,计算![]() 即可.
即可.
解:(1)证明:过点![]() 作
作![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,如图所示;
,如图所示;
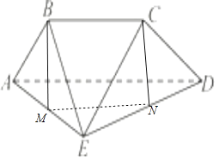
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,![]() ,
,
∴![]() ;
;
由题意知![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ;
;
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ;
;
(2)由已知,![]() 、
、![]() 互相垂直,以
互相垂直,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,如图所示;
,如图所示;
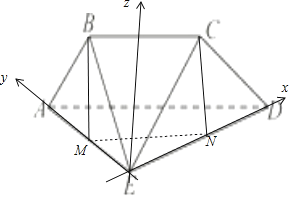
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则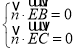 ,
,
即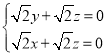 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ;
;
设平面![]() 的法向量为
的法向量为![]() ,则
,则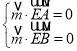 ,
,
易求得![]() ;
;
又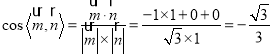 ,
,
∴二面角![]() 的平面角余弦值为
的平面角余弦值为![]() .
.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(![]() )的检测数据,结果统计如下:
)的检测数据,结果统计如下:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 6 | 14 | 18 | 27 | 25 | 10 |
(1)从空气质量指数属于![]() ,
,![]() 的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
(2)已知某企业每天的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() 的关系式为
的关系式为 ,试估计该企业一个月(按30天计算)的经济损失的数学期望.
,试估计该企业一个月(按30天计算)的经济损失的数学期望.