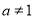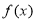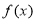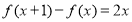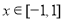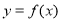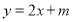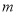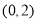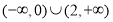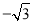题目内容
函数f(x)的定义域为D，满足：①f(x)在D内是单调函数；②存在[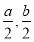
]
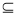D，使得f(x)在[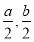]上的值域为[a，b]，那么就称函数y=f(x)为“优美函数”，若函数f(x)=logc(cx－t)(c＞0，c≠1)是“优美函数”，则t的取值范围为( )
A. (0，1) B. (0，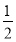
) C. (－∞，
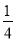) D. (0，)
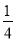D
【解析】
试题分析：由f(x)＝f(x)=logc(cx－t)（c＞0，c≠1）是“优美函数”，知f（x）在其定义域内为增函数，因为f(x)在[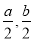
]上的值域为[a，b]，所以方程f（x）= f(x)=logc(cx－t)=
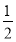x至少有两个根，故cx-t=
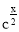，由此能求出t的取值范围．
考点：函数性质的应用.
练习册系列答案
相关题目
