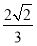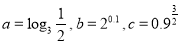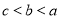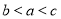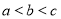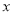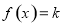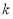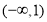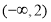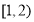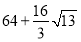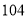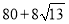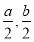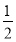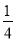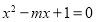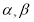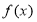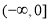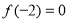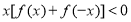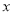题目内容
已知 的图象关于坐标原点对称。
的图象关于坐标原点对称。
(1)求 的值,并求出函数
的值,并求出函数 的零点;
的零点;
(2)若函数 在[0,1]内存在零点,求实数b的取值范围;
在[0,1]内存在零点,求实数b的取值范围;
(3)设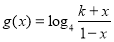 ,已知
,已知 的反函数
的反函数 =
= ,若不等式
,若不等式 在
在 上恒成立,求满足条件的最小整数k的值。
上恒成立,求满足条件的最小整数k的值。
(1)F(x)的零点为x=1;(2)2≤b≤7;(3)满足条件的最小整数k的值是8
【解析】
试题分析:(1)根据函数的图象关于原点对称,可得f(x)是定义在R的奇函数,图象必过原点,即f(0)=0,求出a的值,求出函数F(x)的解析式,解指数方程求求出函数的零点;
(2)函数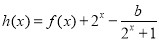 在[0,1]内存在零点,方程(2x)2+2x+1-1-b=0在[0,1]内有解,分析函数b=(2x)2+2x+1-1在[0,1]内的单调性,及端点的函数值符号,进而根据零点存在定理得到结论;
在[0,1]内存在零点,方程(2x)2+2x+1-1-b=0在[0,1]内有解,分析函数b=(2x)2+2x+1-1在[0,1]内的单调性,及端点的函数值符号,进而根据零点存在定理得到结论;
(3)由不等式f-1(x)≤g(x)在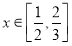 上恒成立,利用基本不等式可求出满足条件的k的范围,进而求出最小整数k的值.
上恒成立,利用基本不等式可求出满足条件的k的范围,进而求出最小整数k的值.
试题解析:(1)由题意知f(x)是R上的奇函数,

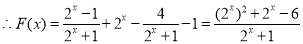
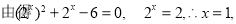
即F(x)的零点为x=1. 4分
(2)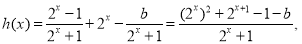
由题设知h(x)=0在[0,1]内有解,
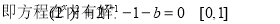
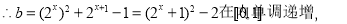
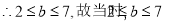
 在[0,1]内存在零点 8分
在[0,1]内存在零点 8分
(3)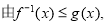
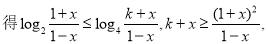
显然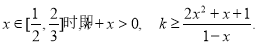
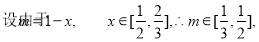

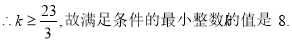 14分
14分
考点:函数的性质的综合应用.

练习册系列答案
相关题目