题目内容
已知函数f(x)=2x-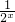 .
.
(1)若f(x)=2,求x的值;
(2)若对于t∈[1,2]时,不等式2tf(2t)+mf(t)≥0恒成立,求实数m的取值范围.
解:(1)f(x)=2即2x-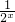 =2,得4x-2×2x-1=0,∴2x=1±
=2,得4x-2×2x-1=0,∴2x=1± ,
,
又2x>0,∴2x=1+ ,
,
∴x=log2(1+ ).
).
(2)∵2t(22t-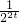 )+m(2t-
)+m(2t-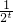 )≥0,
)≥0,
∴2t(2t-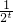 )(2t+
)(2t+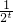 )+m(2t-
)+m(2t-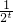 )≥0,∵t∈[1,2],∴2t>
)≥0,∵t∈[1,2],∴2t>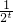 ,
,
∴4t+1+m≥0恒成立,即m≥-(4t+1)恒成立,问题等价于m大于等于-(4t+1)的最大值-5,
∴m≥-5,
因此m的取值范围为[-5,+∞).
分析:(1)f(x)=2即2x-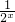 =2,先解2x,再解x值,注意2x>0;
=2,先解2x,再解x值,注意2x>0;
(2)不等式2tf(2t)+mf(t)≥0恒成立,通过整理变形转化为4t+1+m≥0恒成立,分离参数m后转化为求函数最值问题解决;
点评:本题考查函数恒成立问题及指数方程的求解,考查学生的分析问题解决问题的能力,恒成立问题往往转化为求函数最值问题解决,或分离参数后再求函数最值.
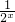 =2,得4x-2×2x-1=0,∴2x=1±
=2,得4x-2×2x-1=0,∴2x=1± ,
,又2x>0,∴2x=1+
 ,
,∴x=log2(1+
 ).
).(2)∵2t(22t-
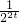 )+m(2t-
)+m(2t-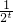 )≥0,
)≥0,∴2t(2t-
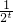 )(2t+
)(2t+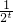 )+m(2t-
)+m(2t-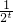 )≥0,∵t∈[1,2],∴2t>
)≥0,∵t∈[1,2],∴2t>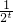 ,
,∴4t+1+m≥0恒成立,即m≥-(4t+1)恒成立,问题等价于m大于等于-(4t+1)的最大值-5,
∴m≥-5,
因此m的取值范围为[-5,+∞).
分析:(1)f(x)=2即2x-
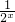 =2,先解2x,再解x值,注意2x>0;
=2,先解2x,再解x值,注意2x>0;(2)不等式2tf(2t)+mf(t)≥0恒成立,通过整理变形转化为4t+1+m≥0恒成立,分离参数m后转化为求函数最值问题解决;
点评:本题考查函数恒成立问题及指数方程的求解,考查学生的分析问题解决问题的能力,恒成立问题往往转化为求函数最值问题解决,或分离参数后再求函数最值.

练习册系列答案
相关题目