题目内容
有下列命题,其中为假命题的是( )A.
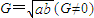 是a,G,b成等比数列的充分非必要的条件
是a,G,b成等比数列的充分非必要的条件B.若角α,β满足cosαcosβ=1,则sin(α+β)=0
C.当a≥1时,不等式|x-4|+|x-3|<a的解集非空
D.函数y=sinx+sin|x|的值域是[-2,2]
【答案】分析:根据等比中项的定义及等比数列的性质,可以判断A的真假;根据余弦函数的性质,及两角和的正弦公式,我们可以求出B的真假;根据绝对值不等式的几何意义,我们可以判断C的真假,根据正弦型函数及分段函数值域的确定方法,可以判断D的真假,进而得到答案.
解答:解:若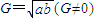 ,则a,G,b成等比数列,若a,G,b成等比数列,则
,则a,G,b成等比数列,若a,G,b成等比数列,则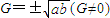 ,
,
故A中,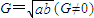 是a,G,b成等比数列的充分非必要的条件为真命题;
是a,G,b成等比数列的充分非必要的条件为真命题;
若角α,β满足cosαcosβ=1,则cosα=cosβ=1或cosα=cosβ=-1,此时sin(α+β)=0都成立,故B为真命题;
不等式|x-4|+|x-3|≥1恒成立,故当a=1时,不等式|x-4|+|x-3|<a的解集为空集,故C为假命题;
当x≤0时,函数y=sinx+sin|x|=0恒成立,当x>0时,函数y=sinx+sin|x|=2sinx∈[-2,2],
故D中,函数y=sinx+sin|x|的值域是[-2,2]为真命题;
故选C
点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,正弦函数的值域,绝对值不等式的解法,等比关系的确定,其中根据上述知识点,分别判断出四个答案中四个命题的真假,是解答本题的关键.
解答:解:若
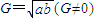 ,则a,G,b成等比数列,若a,G,b成等比数列,则
,则a,G,b成等比数列,若a,G,b成等比数列,则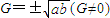 ,
,故A中,
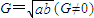 是a,G,b成等比数列的充分非必要的条件为真命题;
是a,G,b成等比数列的充分非必要的条件为真命题;若角α,β满足cosαcosβ=1,则cosα=cosβ=1或cosα=cosβ=-1,此时sin(α+β)=0都成立,故B为真命题;
不等式|x-4|+|x-3|≥1恒成立,故当a=1时,不等式|x-4|+|x-3|<a的解集为空集,故C为假命题;
当x≤0时,函数y=sinx+sin|x|=0恒成立,当x>0时,函数y=sinx+sin|x|=2sinx∈[-2,2],
故D中,函数y=sinx+sin|x|的值域是[-2,2]为真命题;
故选C
点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,正弦函数的值域,绝对值不等式的解法,等比关系的确定,其中根据上述知识点,分别判断出四个答案中四个命题的真假,是解答本题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
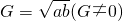 是a,G,b成等比数列的充分非必要的条件
是a,G,b成等比数列的充分非必要的条件