题目内容
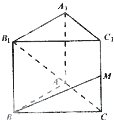 (理)如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是( )
(理)如图,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是( )分析:设三棱柱ABC-A1B1C1的棱长等于2,延长MC1到N使MN=BB1,连接AN.可得∠AB1N(或其补角)就是异面直线AB1和BM所成角,然后在△AB1N中分别算出三条边的长,利用余弦定理得cos∠AB1N=0,可得∠AB1N=90°,从而得到异面直线AB1和BM所成角.
解答: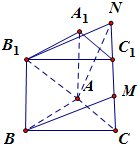 解:设三棱柱ABC-A1B1C1的棱长等于2,延长MC1到N使MN=BB1,连接AN,则
解:设三棱柱ABC-A1B1C1的棱长等于2,延长MC1到N使MN=BB1,连接AN,则
∵MN∥BB1,MN=BB1,∴四边形BB1NM是平行四边形,可得B1N∥BM
因此,∠AB1N(或其补角)就是异面直线AB1和BM所成角
∵Rt△B1C1N中,B1C1=2,C1N=1,∴B1N=
∵Rt△ACN中,AC=2,CN=3,∴AN=
又∵正方形AA1B1B中,AB1=2
∴△AB1N中,cos∠AB1N=
=0,可得∠AB1N=90°
即异面直线AB1和BM所成角为90°
故选:A
 解:设三棱柱ABC-A1B1C1的棱长等于2,延长MC1到N使MN=BB1,连接AN,则
解:设三棱柱ABC-A1B1C1的棱长等于2,延长MC1到N使MN=BB1,连接AN,则∵MN∥BB1,MN=BB1,∴四边形BB1NM是平行四边形,可得B1N∥BM
因此,∠AB1N(或其补角)就是异面直线AB1和BM所成角
∵Rt△B1C1N中,B1C1=2,C1N=1,∴B1N=
| 5 |
∵Rt△ACN中,AC=2,CN=3,∴AN=
| 13 |
又∵正方形AA1B1B中,AB1=2
| 2 |
∴△AB1N中,cos∠AB1N=
| 5+8-13 | ||||
2×
|
即异面直线AB1和BM所成角为90°
故选:A
点评:本题在所有棱长均相等的正三棱柱中,求异面直线所成的角大小,着重考查了正三棱柱的性质、余弦定理和异面直线所成角求法等知识,属于基础题.

练习册系列答案
相关题目

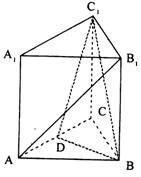

 (2009四川卷理)如图,已知正三棱柱
(2009四川卷理)如图,已知正三棱柱