Question

【题目】已知函数且a≠1,函数.

（1）判断并证明f(x)和g(x)的奇偶性;

（2）求g(x)的值域;

（3）若x∈R,都有|f(x)|≥|g(x)|成立,求a的取值范围.

Answer 1

【答案】（1）答案见解析.（2）.（3）.

.

【解析】

（1）利用定义判断函数的奇偶性得解；（2）利用双勾函数的图象和性质求出值域；（3）考虑到函数f(x),g(x)都是奇函数,故只需保证x≥0时都有|f(x)|≥|g(x)|即可,再对a分两种情况a＞1和0＜a＜1讨论，利用导数求出实数a的取值范围是.

（1）首先,f(x),g(x)的定义域都是R,是关于原点对称的,

其次,f(﹣x)=a﹣x﹣a﹣(﹣x)=﹣(ax﹣a﹣x)=﹣f(x),,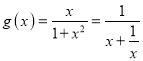

∴函数f(x),g(x)均为奇函数;

（2）当x=0时,g(0)=0;

当x≠0时,,

令,则由双勾函数的性质可知,t∈(﹣∞,﹣2]∪[2,+∞),

∴,即此时,

综上,函数g(x)的值域为;

（3）考虑到函数f(x),g(x)都是奇函数,故只需保证x≥0时都有|f(x)|≥|g(x)|即可,

这是因为当x＜0时,|f(x)|=|f(﹣x)|,|g(x)|=|g(﹣x)|,

①先考虑a＞1的情形,此时f(x)=ax﹣a﹣x≥1﹣1=0,g(x)≥0,

因此只需当x≥0时,f(x)﹣g(x)≥0恒成立即可,

令,则,

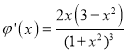令,则,

当时,φ′(x)>0,即φ(x)单增,故此时φ(x)min=φ(0)=﹣1;

当时,,故x=0时,φ(x)气的最小值﹣1,

若,则h′(x)=(ax+a﹣x)lna+φ(x)≥2lna﹣1≥0,

∴h(x)单增,故h(x)≥h(0)=0,符合题设;

若,则,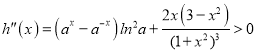

且0＜x＜1时,,h′(x)单增,

故由零点存在性定理可知存在x0∈(0,1),使得h′(x0)=0,

且x∈(0,x0)时h′(x)＜0,h(x)单减,当x∈(x0,1)时h′(x)＞0,h(x)单增,

则h(x0)<h(0)=0,不符合题意,

故;

②再考虑0＜a＜1的情形,此时,

此时的与①中的a地位等价,同①理可知,即,

综合①②可知,实数a的取值范围是.