题目内容
设λ>0,点A的坐标为(1,1),点B在抛物线y=x2上运动,点Q满足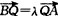 ,经过点Q与x轴垂直的直线交抛物线于点M,点P满足
,经过点Q与x轴垂直的直线交抛物线于点M,点P满足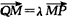 ,求点P的轨迹方程。
,求点P的轨迹方程。
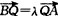 ,经过点Q与x轴垂直的直线交抛物线于点M,点P满足
,经过点Q与x轴垂直的直线交抛物线于点M,点P满足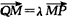 ,求点P的轨迹方程。
,求点P的轨迹方程。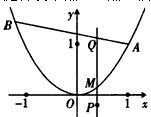
解:由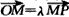 知Q,M,P三点在同一条垂直于x轴的直线上,
知Q,M,P三点在同一条垂直于x轴的直线上,
故可设P(x,y),Q(x,y0),M(x,x2),
则x2-y0=λ(y-x2),
即y0=(1+λ)x2-λy ①
再设B(x1,y1),由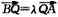
即(x-x1,y0-y1)=λ(1-x,1-y0),
解得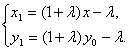 ②
②
将①式代入②式,消去y0,
得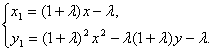 ③
③
又点B在抛物线y=x2上,所以y1=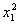 ,再将③式代入y1=
,再将③式代入y1=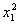
得(1+λ)2x2-λ(1+λ)y-λ=((1+λ)x-λ)2,
(1+λ)2x2-λ(1+)y-λ=(1+λ)2x2-2λ(1+λ)x+λ2,
2(1+λ)x-λ(1+λ)y-λ(1+λ)=0
因λ>0,两边同除以λ(1+λ),得2x-y-1=0
故所求点P的轨迹方程y=2x-1。

练习册系列答案
相关题目
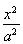
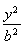
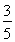
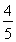
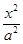 +
+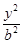 =1(a>b>0)上一点A关于原点的对称点为B, F为其右焦点, 若AF⊥BF, 设∠ABF=
=1(a>b>0)上一点A关于原点的对称点为B, F为其右焦点, 若AF⊥BF, 设∠ABF=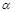 , 且
, 且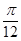 ,
,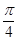 ], 则该椭圆离心率的取值范围为 (
)
], 则该椭圆离心率的取值范围为 (
)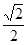 ,1 ) B.[
,1 ) B.[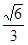 ] C.[
] C.[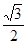
 +
+ =1(a>b>0)上一点A关于原点的对称点为B,F为其右焦点,若AF⊥BF,设∠ABF=
=1(a>b>0)上一点A关于原点的对称点为B,F为其右焦点,若AF⊥BF,设∠ABF= ,且
,且 ,
, ],则该椭圆离心率的取值范围为
],则该椭圆离心率的取值范围为  ,1 ) B.[
,1 ) B.[ ]
]  ]
]