题目内容
10.已知($\sqrt{x}$+$\frac{2}{{x}^{2}}$)n的展开式中所有的二次项系数之和为1024,则展开式中的常数项是144.分析 依题意得,由二项式系数和2n=1024,求得n的值,求出展开式的通项公式,再令通项公式中x的幂指数等于0,求得r的值,即可求得展开式中的常数项.
解答 解:依题意得,由二项式系数和2n=1024,解得n=10;
由于展开式的通项公式为 Tr+1=${C}_{10}^{r}•{2}^{r}•{x}^{5-\frac{5}{2}r}$
令5-$\frac{5}{2}$r=0,解得r=2,
∴展开式中的常数项为${C}_{10}^{2}•{2}^{2}$=144.
故答案为:144.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
20.给定y与x的一组样本数据,求得相关系数r=-0.990,则( )
| A. | y与x负线性相关 | B. | y与x正线性相关 | ||
| C. | y与x的线性相关性较强 | D. | y与x的相关性很强 |
10.现有一段长为18m的铁丝,要把它围成一个底面一边长为另一边长2倍的长方体形状的框架,当长方体体积最大时,底面的较短边长是( )
| A. | 1 m | B. | 1.5 m | C. | 0.75 m | D. | 0.5 m |
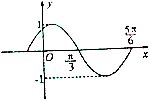 如图函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)图象的一部分,则f($\frac{π}{4}$)的值为$\frac{1}{2}$.
如图函数y=Asin(ωx+φ)(A>0,ω>0,|φ|≤$\frac{π}{2}$)图象的一部分,则f($\frac{π}{4}$)的值为$\frac{1}{2}$.