题目内容
若圆x2＋y2－4x－4y－10＝0上至少有三个不同点到直线l：ax＋by＝0的距离为2
，则直线l的斜率的取值范围是________．
，则直线l的斜率的取值范围是________．[2－，2＋]
，2＋]圆x2＋y2－4x－4y－10＝0可转化为(x－2)2＋(y－2)2＝(3)2，∴圆心的坐标为(2,2)，半径为3，要求圆上至少有三个不同的点到直线l：ax＋by＝0的距离为2，则圆心到直线l的距离应小于等于，
∴
≤，∴
2＋4
＋1≤0，∴－2－≤
≤－2＋，又直线l的斜率k＝－，∴2－≤k≤2＋，即直线l的斜率的取值范围是[2－，2＋]．
)2，∴圆心的坐标为(2,2)，半径为3，要求圆上至少有三个不同的点到直线l：ax＋by＝0的距离为2，则圆心到直线l的距离应小于等于，∴
≤，∴2＋4＋1≤0，∴－2－≤≤－2＋，又直线l的斜率k＝－，∴2－≤k≤2＋，即直线l的斜率的取值范围是[2－，2＋]．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
上的点到直线
的距离的最小值和最大值．
的倾斜角为 ．
∪
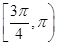
上两点
的坐标分别为
,且直线
垂直，则
的值为（ ）
的倾斜角和斜率分别是（ ）
，不存在
，不存在
y＋2＝0的倾斜角的范围是________．
的倾斜角为钝角，则实数
的取值范围是 ．
y-1=0垂直的直线的倾斜角为________．