题目内容
【题目】已知椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,其离心率
,其离心率![]() ,以原点为圆心,椭圆的半焦距为半径的圆与直线
,以原点为圆心,椭圆的半焦距为半径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 交
交![]() 于
于![]() 两点,
两点, ![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积
的面积![]() 满足:
满足: ![]() ,求直线
,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1) 利用题意列出方程组求解![]() 的值即可求得椭圆的标准方程;
的值即可求得椭圆的标准方程;
(2)设出直线方程,联立直线与椭圆的方程,结合点到直线的距离公式得到关于![]() 的方程,解方程即可球的最终结果,注意直线斜率不存在的情况.
的方程,解方程即可球的最终结果,注意直线斜率不存在的情况.
试题解析:
(I)由题意得, 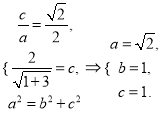 故椭圆
故椭圆![]() 的方程为
的方程为![]() .
.
(II)由于直线![]() 的倾斜角不可为零,所以设直线
的倾斜角不可为零,所以设直线![]() 的方程为
的方程为![]() ,
,
与![]() 联立可得
联立可得![]()
设![]() 则
则![]() 可得
可得
![]()
设![]() , 又
, 又![]() 所以
所以![]() 因为
因为![]() 在
在![]() 上, 故
上, 故
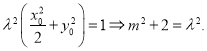 --------------------①
--------------------①
设![]() 为点
为点![]() 到直线
到直线![]() 的距离,
的距离, ![]() 为点
为点![]() 到直线
到直线![]() 的距离,则
的距离,则
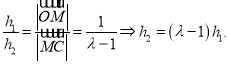
又由点到直线的距离公式得, ![]()
而![]() 所以
所以
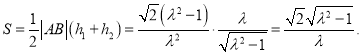
由题意知, ![]() 所以
所以![]() 将
将![]() 代入①式
代入①式![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目