题目内容
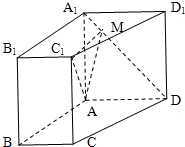 (2005•南汇区一模)(理)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ABC=90°,AB=5,BC=2,AD=8,异面直线AC1与A1D互相垂直.
(2005•南汇区一模)(理)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ABC=90°,AB=5,BC=2,AD=8,异面直线AC1与A1D互相垂直.(1)求直棱柱棱AA1的长;
(2)若点M在线段A1D上,AM⊥A1D,求直线AD与平面AMC1所成的角的大小.
分析:(1)根据题意建立空间直角坐标系写出点的坐标,即可得到有关向量的坐标,再利用异面直线AC1与A1D互相垂直,
⊥
,即
•
=0,进而得到答案.
(2)由(1)可得
•
=0,即A1D⊥AC1,再结合题意可得:A1D⊥平面AC1M,可得∠MAD即为直线AD与平面AMC1所成的角,再利用题中的条件与解三角形的有关知识可得答案.
| AC1 |
| A1D |
| AC1 |
| A1D |
(2)由(1)可得
| A1D |
| AC1 |
解答:解:(1)因为在直四棱柱ABCD-A1B1C1D1中,∠BAD=90°,
所以AD,AB,AA1三条直线两两垂直,
所以以A为坐标原点以AB、AD、AA1所在直线分别x轴、y轴、Z轴建立直角坐标系,设棱AA1的长为a,(a>0)
则有A (0,0,0),B (5,0,0),C(5,2,0),D(0,8,0),A1(0,0,a),B1(5,0,a),C1(5,2,a),D1(0,8,a),
∴
=(5,2,a),
=(0,8,-a),(3分)
又因为异面直线AC1与A1D互相垂直,
所以
⊥
,即
•
=0,(6分)
所以可得:a=4,
故棱AA1的长为4.(8分)
(2)由(1)知
=(0,8,-4),
=(5,2,4),
所以
•
=0,即A1D⊥AC1,
又因为AM⊥A1D,AM∩AC1=A,
所以A1D⊥平面AC1M,
所以∠MAD即为直线AD与平面AMC1所成的角.(10分)
因为AA1=4,AD=8,AM⊥A1D,
所以AM=
,
所以cos∠MAD=
=
=
(12分)
所以直线AD与平面AMC1所成的角的大小是arccos
.(13分)
所以AD,AB,AA1三条直线两两垂直,
所以以A为坐标原点以AB、AD、AA1所在直线分别x轴、y轴、Z轴建立直角坐标系,设棱AA1的长为a,(a>0)
则有A (0,0,0),B (5,0,0),C(5,2,0),D(0,8,0),A1(0,0,a),B1(5,0,a),C1(5,2,a),D1(0,8,a),
∴
| AC1 |
| A1D |
又因为异面直线AC1与A1D互相垂直,
所以
| AC1 |
| A1D |
| AC1 |
| A1D |
所以可得:a=4,
故棱AA1的长为4.(8分)

(2)由(1)知
| A1D |
| AC1 |
所以
| A1D |
| AC1 |
又因为AM⊥A1D,AM∩AC1=A,
所以A1D⊥平面AC1M,
所以∠MAD即为直线AD与平面AMC1所成的角.(10分)
因为AA1=4,AD=8,AM⊥A1D,
所以AM=
8
| ||
| 5 |
所以cos∠MAD=
| AM |
| AD |
| ||||
| 8 |
| ||
| 5 |
所以直线AD与平面AMC1所成的角的大小是arccos
| ||
| 5 |
点评:本题主要考查利用向量证明线线垂直,进而得到线面垂直,并且考查了线面角的求解,解决此类问题的关键是熟练掌握几何体的结构特征与向量之间的有关运算.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 (2005•南汇区一模)已知数列{an},
(2005•南汇区一模)已知数列{an},