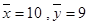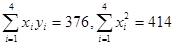题目内容
一机器可以按各种不同速度运转,其生产物件有一些会有缺陷,每小时生产有缺陷物件的多少随机器运转速度而变化,用x表示转速(单位:转/秒),用y表示每小时生产的有缺陷物件个数,现观测得到(x,y)的4组观测值为(8,5),(12,8),(14,9),(16,11).
(Ⅰ)假定y与x之间有线性相关关系,求y与x之间的回归直线方程;
(Ⅱ)若实际生产中所容许的每小时最大有缺陷物件数为l0,则机器的速度不得超过多少转/秒?(精确到1)
(Ⅰ)假定y与x之间有线性相关关系,求y与x之间的回归直线方程;
(Ⅱ)若实际生产中所容许的每小时最大有缺陷物件数为l0,则机器的速度不得超过多少转/秒?(精确到1)
分析:(Ⅰ)先求出横标和纵标的平均数,得到这组数据的样本中心点,利用最小二乘法求出线性回归方程的系数,代入样本中心点求出a的值,写出线性回归方程.
(Ⅱ)由实际生产中所容许的每小时最大有缺陷物件数为l0,建立不等式进行求解即可.
(Ⅱ)由实际生产中所容许的每小时最大有缺陷物件数为l0,建立不等式进行求解即可.
解答:解:(Ⅰ)设回归直线方程为
=bx+a,则
=
=
,
=
=
,b=
=
,a=
-b
=-
,
故所求的回归方程为
=
x-
.
(Ⅱ)由
x-
≤10得x≤
≈15,故机器的速度不得超过15转/秒.
| ∧ |
| y |
. |
| x |
| 8+12+14+16 |
| 4 |
| 25 |
| 2 |
. |
| y |
| 5+8+9+11 |
| 4 |
| 33 |
| 4 |
| |||||||
|
| 51 |
| 70 |
. |
| y |
. |
| x |
| 6 |
| 7 |
故所求的回归方程为
| ∧ |
| y |
| 51 |
| 70 |
| 6 |
| 7 |
(Ⅱ)由
| 51 |
| 70 |
| 6 |
| 7 |
| 760 |
| 51 |
点评:本题考查线性回归方程的求法和应用,本题解题的关键是利用最小二乘法求出线性回归方程的系数,考查学生的运算能力.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
一机器可以按各种不同速度运转,其生产之物件有一些会有缺点,每小时生产有缺点的物件的多寡,随机器运转速度而变化,下列为其试验结果.
速度(转/秒) | 8 | 12 | 14 | 16 |
每小时生产有缺点物件数 | 5 | 8 | 9 | 11 |
(1)求出机器速度的影响每小时生产有缺点物件数的回归直线方程.
(2)若实际生产中所容许的每小时最大缺点物件数为10,那么机器速度不得超过多少转/秒?
一机器可以按各种不同速度运转,其生产的产品有一些会有缺点,每小时生产有缺点的产品数随机器运转速度的不同而变化。下表为其试验数据:
|
速度(x转/秒) |
|
||
|
8 |
6 |
||
|
9 |
8 |
||
|
10 |
10 |
||
|
13 |
12 |
(1)、画出散点图;
(2)、求机器运转速度与每小时生产有缺点的产品数之间的回归方程;(系数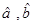 用分数表示)
用分数表示)
(3)、若实际生产所允许的每小时生产有缺点的产品数不超过10件,那么机器的速度每秒不超过多少转?