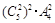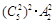题目内容
从5位男教师和4位女教师中选出3位教师,派到3个班担任班主任(每班1位班主任),要求这3位班主任中男、女教师都要有,则不同的选派方案共有:
| A.210种 | B.420种 | C.630种 | D.840种 |
B
解析试题分析:题目要求有男女教师九人选三个到3个班担任班主任是三个元素在九个位置排列,要求这3位班主任中男女教师都有,则选的都是男教师和选的都是女教师不合题意就,需要从总数中去掉.解:∵共有男女教师九人选三个到3个班担任班主任共有A93种结果,要求这3位班主任中男女教师都有,则选的都是男教师和选的都是女教师不合题意,选的都是男教师有A53种结果,选的都是女教师有A43种结果,∴满足条件的方案有A93-(A53+A43)=420,故选B.
考点:排列与组合问题
点评:排列与组合问题要区分开,若题目要求元素的顺序则是排列问题,排列问题要做到不重不漏,有些题目带有一定的约束条件,解题时要先考虑有限制条件的元素,属于中档题

练习册系列答案
相关题目
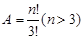 ,则A是( )
,则A是( )
A.C | B.C | C.A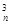 | D.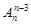 |
将2个相同的 和2个相同的
和2个相同的 共4个字母填在
共4个字母填在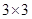 的方格内,每个小方格内至多填1个字母,若使相同字母既不同行也不同列,则不同的填法种数为 ( )
的方格内,每个小方格内至多填1个字母,若使相同字母既不同行也不同列,则不同的填法种数为 ( )
| A.196 | B.197 | C.198 | D.199 |
若 =
=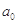 +
+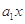 +
+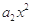 +…+
+…+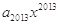 (x∈R),则
(x∈R),则 +
+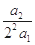 +
+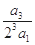 +…+
+…+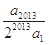
A.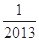 | B.-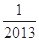 | C.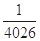 | D.-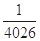 |
某市有7条南北向街道,5条东西向街道.图中共有m个矩形,从A点走到B点最短路线的走法有n种,则m,n的值分别为( )
| A.m=90,n=210 | B.m="210,n=210" |
| C.m=210,n=792 | D.m=90,n=792 |
如图所示,使电路接通,开关不同的开闭方式有( )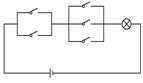
| A.11种 | B.20种 |
| C.21种 | D.12种 |
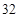

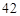

 的二项展开式中x7项的系数为﹣10,则a= .
的二项展开式中x7项的系数为﹣10,则a= .