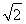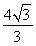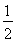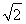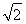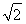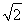题目内容
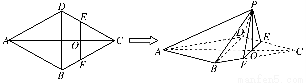
如图，在三棱柱ABC－A1B1C1中，侧面AA1C1C⊥底面ABC，AA1＝A1C＝AC＝2，AB＝BC，AB⊥BC，O为AC中点．
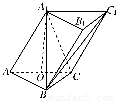
(1)证明：A1O⊥平面ABC；
(2)若E是线段A1B上一点，且满足VE－BCC1＝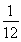
·VABC－A1B1C1，求A1E的长度．
（1）见解析（2）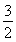
【解析】(1)证明：∵AA1＝A1C＝AC＝2，且O为AC中点，
∴A1O⊥AC，又∵侧面AA1C1C⊥底面ABC，侧面AA1C1C∩底面ABC＝AC，A1O?平面A1AC，
∴A1O⊥平面ABC.
(2)∵VE－BCC1＝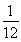
VABC－A1B1C1＝
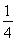VA1－BCC1，∴BE＝
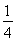BA1，即A1E＝
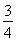A1B.
连接OB，在Rt△A1OB中，A1O⊥OB，A1O＝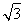
，BO＝1，故A1B＝2，则A1E的长度为.
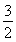练习册系列答案
相关题目
