题目内容
已知函数f(x)=ax2+1nx(a∈R).
(I)当 时,求f(x)在区间[1,e]上的最大值和最小值;
时,求f(x)在区间[1,e]上的最大值和最小值;
(II)如果在公共定义域D上的函数g(x),f1(x),f2(x)满足f1(x)<g(x)<f2(x),那么就称g(x)为f1(x)、f2(x)的“活动函数”,已知函数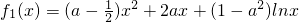 ,
,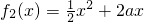 ,若在区间(1,+∞)上,函数f(x)是f1(x)、f2(x)的“活动函数”,求实数a的取范围.
,若在区间(1,+∞)上,函数f(x)是f1(x)、f2(x)的“活动函数”,求实数a的取范围.
解:(I)当 时,函数f(x)=
时,函数f(x)= x2+1nx,定义域为(0,+∞)
x2+1nx,定义域为(0,+∞)
求导函数可得f′(x)=x+ >0在(0,+∞)上恒成立,所以函数在(0,+∞)上单调增
>0在(0,+∞)上恒成立,所以函数在(0,+∞)上单调增
∴f(x)在区间[1,e]上单调增
∵f(1)= ,f(e)=
,f(e)=
∴f(x)在区间[1,e]上的最大值为 和最小值为
和最小值为 ;
;
(II)由题意,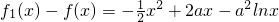 <0且
<0且 >0,在区间(1,+∞)上恒成立
>0,在区间(1,+∞)上恒成立
令 (x>1),则g′(x)=-
(x>1),则g′(x)=- ,∴函数g(x)在(1,+∞)上单调减
,∴函数g(x)在(1,+∞)上单调减
∵g(1)= +2a,∴
+2a,∴ +2a≤0,∴a≤
+2a≤0,∴a≤ ;
;
令h(x)=f2(x)-f(x)= ,则h′(x)=
,则h′(x)=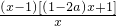 ,
,
又由x∈(1,+∞),且a≤ ,分析易得h′(x)=
,分析易得h′(x)=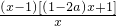 <0,
<0,
即h(x)在(1,+∞)上为减函数,则h(x)max=h(1),
只要使h(1)≤0即可,即a- -2a≤0,解可得,a≥-
-2a≤0,解可得,a≥- ,
,
综合可得,- ≤a≤
≤a≤ .
.
分析:(I)当 时,函数f(x)=
时,函数f(x)= x2+1nx,定义域为(0,+∞),确定f(x)在区间[1,e]上单调增,由此可得结论;
x2+1nx,定义域为(0,+∞),确定f(x)在区间[1,e]上单调增,由此可得结论;
(II)由题意,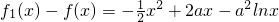 <0且
<0且 >0,在区间(1,+∞)上恒成立,分别确定函数的最小与最大,即可求得a的取值范围.
>0,在区间(1,+∞)上恒成立,分别确定函数的最小与最大,即可求得a的取值范围.
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查新定义,考查学生分析解决问题的能力,属于中档题.
 时,函数f(x)=
时,函数f(x)= x2+1nx,定义域为(0,+∞)
x2+1nx,定义域为(0,+∞)求导函数可得f′(x)=x+
 >0在(0,+∞)上恒成立,所以函数在(0,+∞)上单调增
>0在(0,+∞)上恒成立,所以函数在(0,+∞)上单调增∴f(x)在区间[1,e]上单调增
∵f(1)=
 ,f(e)=
,f(e)=
∴f(x)在区间[1,e]上的最大值为
 和最小值为
和最小值为 ;
;(II)由题意,
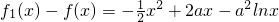 <0且
<0且 >0,在区间(1,+∞)上恒成立
>0,在区间(1,+∞)上恒成立令
 (x>1),则g′(x)=-
(x>1),则g′(x)=- ,∴函数g(x)在(1,+∞)上单调减
,∴函数g(x)在(1,+∞)上单调减∵g(1)=
 +2a,∴
+2a,∴ +2a≤0,∴a≤
+2a≤0,∴a≤ ;
;令h(x)=f2(x)-f(x)=
 ,则h′(x)=
,则h′(x)=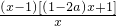 ,
,又由x∈(1,+∞),且a≤
 ,分析易得h′(x)=
,分析易得h′(x)=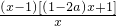 <0,
<0,即h(x)在(1,+∞)上为减函数,则h(x)max=h(1),
只要使h(1)≤0即可,即a-
 -2a≤0,解可得,a≥-
-2a≤0,解可得,a≥- ,
,综合可得,-
 ≤a≤
≤a≤ .
.分析:(I)当
 时,函数f(x)=
时,函数f(x)= x2+1nx,定义域为(0,+∞),确定f(x)在区间[1,e]上单调增,由此可得结论;
x2+1nx,定义域为(0,+∞),确定f(x)在区间[1,e]上单调增,由此可得结论;(II)由题意,
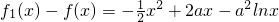 <0且
<0且 >0,在区间(1,+∞)上恒成立,分别确定函数的最小与最大,即可求得a的取值范围.
>0,在区间(1,+∞)上恒成立,分别确定函数的最小与最大,即可求得a的取值范围.点评:本题考查导数知识的运用,考查函数的单调性与最值,考查新定义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目