Question

已知复数z且|z|=1，则|z-2-2i|的最小值是（　　）

• A．2

  2

• B．2

  2

  -1
• C．2

  2

  +1
• D．

  2

  -1

Answer 1

分析：利用复数模的几何意义求解运算．

解答：解：∵|z|=1，则z对应的点Z在以原点为圆心，以1为半径的圆上，
如图，

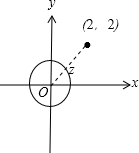
∴|z-2-2i|的最小值是复数2+2i对应的点（2，2）到原点的距离减去半径1，
即

22+22

-1=2

2

-1．
故选B．

点评：本题考查了复数模的几何意义，考查了数形结合的解题思想方法，是基础题．