题目内容
设等差数列![]() 的首项为a,公差为d ( d>0 ). 数列
的首项为a,公差为d ( d>0 ). 数列![]() 定义如下:对于正整数m,
定义如下:对于正整数m,![]() 是使不等式
是使不等式![]() 成立的所有n中的最大值.(例如:b1是使不等式
成立的所有n中的最大值.(例如:b1是使不等式![]() 成立的所有n中的最大值,b2是使不等式
成立的所有n中的最大值,b2是使不等式![]() 成立的所有n中的最大值,……,如此类推).
成立的所有n中的最大值,……,如此类推).
(1)若![]() ,
,![]() 求
求![]() ;
;
(2)若![]() ,求数列
,求数列![]() 前2m项的和;
前2m项的和;
(3)是否存在等差数列![]() ,使得
,使得![]() ,若存在,求a和d的范围;
,若存在,求a和d的范围;
若不存在,请说明理由.
(1)当m=5时,由![]() ,解得
,解得![]() ,则n的最大整数为10,
,则n的最大整数为10,
所以 ![]() =10 . ……………………2分
=10 . ……………………2分
(2)由![]() ,解得
,解得![]() .
.
当m为奇数时,n的最大整数为![]() ;
;
当m为偶数时,n的最大整数为![]() , 所以
, 所以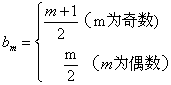 . …………………5分
. …………………5分
![]()
=![]() =
=![]() . …………………………………………8分
. …………………………………………8分
(3))假设存在等差数列![]() ,使得
,使得![]() 。由
。由![]() ,解得
,解得![]() 。因
。因![]() 是使不等式
是使不等式![]() 成立的所有n中的最大值,故
成立的所有n中的最大值,故
![]() 对任意正整数m都成立,变形整理可得
对任意正整数m都成立,变形整理可得![]() (★)对任意正整数m都成立. …………………………11分
(★)对任意正整数m都成立. …………………………11分
当1-3d=0即d=![]() 时,要使(★)对任意正整数m都成立,还需
时,要使(★)对任意正整数m都成立,还需![]() 成立,即
成立,即
![]() ,故当d=
,故当d=![]() ,
,![]() 时,满足题意,所以存在等差数列
时,满足题意,所以存在等差数列![]() ;
;
②当1-3d>0即0<d<![]() 时, 不等式(★)变为
时, 不等式(★)变为![]() ,因
,因![]() 均为确定的实数,所以m为一定范围内的整数,不是所有的正整数,故(★)不等式不是对任意正整数m都成立;
均为确定的实数,所以m为一定范围内的整数,不是所有的正整数,故(★)不等式不是对任意正整数m都成立;
③当1-3d<0即d>![]() 时, 不等式(★)变为
时, 不等式(★)变为![]() ,因
,因![]() 均为确定的实数,所以m为一定范围内的整数,不是所有的正整数,故(★)不等式不是对任意正整数m都成立。
均为确定的实数,所以m为一定范围内的整数,不是所有的正整数,故(★)不等式不是对任意正整数m都成立。
综合上述:存在等差数列![]() 满足题意,此时d=
满足题意,此时d=![]() ,
,![]() . …………………16分
. …………………16分

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目