题目内容
已知圆C:x2+(y-1)2=5,直线l:mx-y+1-m=0
(1)求证:对![]() ,直线l与圆C总有两个不同的交点;
,直线l与圆C总有两个不同的交点;
(2)设l与圆C交于A、B两点,若![]() ,求l的倾角;
,求l的倾角;
(3)求弦AB的中点M的轨迹方程;
(4)若定点P(1,1)分弦AB为![]() ,求此时直线l的方程.
,求此时直线l的方程.
答案:
解析:
解析:
(1)由已知l∶y-1=m(x-1),∴直线l恒过定点P(1,1). ∵12+(1-1)2=1<5, ∴P在圆C内,则直线l与圆C总有两个不同的交点. (2)设A(x1,y2),B(x2,y2),则x1,x2为方程的两实根, ∵ ∴l的倾角为 (3)设M的坐标为(x,y),连结CM,CP,∵C(0,1),P(1,1), 整理得轨迹方程为: (4)∵ 得: ∴直线l的方程为:x-y=0或x+y-2=0.
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
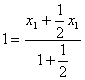 ,∴
,∴ ,直线l与圆C总有两个不同的交点。
,直线l与圆C总有两个不同的交点。 ,求l的倾斜角;
,求l的倾斜角; ,求此时直线l的方程。
,求此时直线l的方程。