题目内容
已知数列{an}为等差数列,a1=2,且其前10项和为65,又正项数列{bn}满足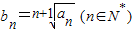
(1)求数列{bn}的通项公式;
(2)比较b1,b2,b3,b4的大小;
(3)求数列{bn}的最大项;
(4)令cn=lgan,数列{cn}是等比数列吗?说明理由.
【答案】分析:(1)设{an}的公差为d,由题设条件得d=1,从而an=n+1,由此可得到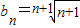 .
.
(2)由题设条件知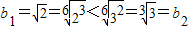
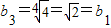 ,
,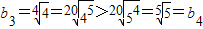 ,由此可知b2>b1=b3>b4
,由此可知b2>b1=b3>b4
(3)由题设猜想当n≥2时,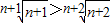 ,再通过导数证明猜想正确,从而得到数列{bn}的最大项是
,再通过导数证明猜想正确,从而得到数列{bn}的最大项是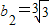 .
.
(4)由题设条件知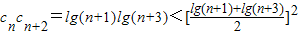 =
= =cn+12,由此知{cn}不是等比数列.
=cn+12,由此知{cn}不是等比数列.
解答:解:(1)设{an}的公差为d
,则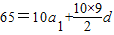
且a1=2,得d=1,从而an=n+1
故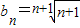 ;
;
(2)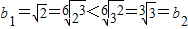
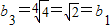 ,
,
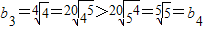
∴b2>b1=b3>b4
(3)由(2)猜想{bn+1}递减,即猜想当n≥2时,
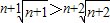
考察函数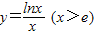 ,当x>e时lnx>1
,当x>e时lnx>1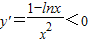
故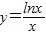 在(e,+∞)上是减函数,而n+1≥3>e
在(e,+∞)上是减函数,而n+1≥3>e
所以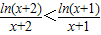 ,即
,即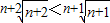
于是猜想正确,因此,数列{bn}的最大项是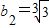 ;
;
(4){cn}不是等比数列
由cn=lgan=lg(n+1)知
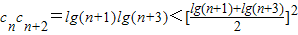
=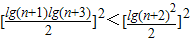
=lg2(n+2)
=cn+12
故{cn}不是等比数列.
点评:本题考查数列性质的综合运用,解题时要认真审题,仔细解答.
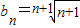 .
.(2)由题设条件知
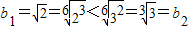
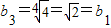 ,
,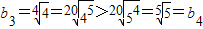 ,由此可知b2>b1=b3>b4
,由此可知b2>b1=b3>b4(3)由题设猜想当n≥2时,
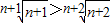 ,再通过导数证明猜想正确,从而得到数列{bn}的最大项是
,再通过导数证明猜想正确,从而得到数列{bn}的最大项是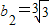 .
.(4)由题设条件知
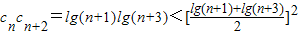 =
= =cn+12,由此知{cn}不是等比数列.
=cn+12,由此知{cn}不是等比数列.解答:解:(1)设{an}的公差为d
,则
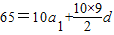
且a1=2,得d=1,从而an=n+1
故
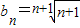 ;
;(2)
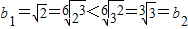
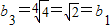 ,
,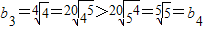
∴b2>b1=b3>b4
(3)由(2)猜想{bn+1}递减,即猜想当n≥2时,
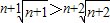
考察函数
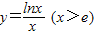 ,当x>e时lnx>1
,当x>e时lnx>1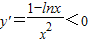
故
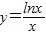 在(e,+∞)上是减函数,而n+1≥3>e
在(e,+∞)上是减函数,而n+1≥3>e所以
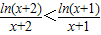 ,即
,即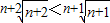
于是猜想正确,因此,数列{bn}的最大项是
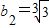 ;
;(4){cn}不是等比数列
由cn=lgan=lg(n+1)知
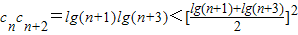
=
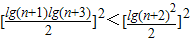
=lg2(n+2)
=cn+12
故{cn}不是等比数列.
点评:本题考查数列性质的综合运用,解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义:在数列{an}中,an>0且an≠1,若
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009=( )
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |

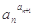 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4