题目内容
若任意a∈A,则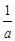 ∈A,就称A是“对偶”集合,则在集合M={-1,0,
∈A,就称A是“对偶”集合,则在集合M={-1,0,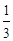 ,
,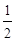 ,1,2,
,1,2,
3,4}的所有非空子集中,“对偶”集合的个数为 .
【答案】
15
【解析】
试题分析:∵由 和3,
和3,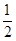 和2,-1,1组成集合,
和2,-1,1组成集合, 和3,
和3,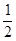 和2都以整体出现,∴有24个集合∵集合为非空集合,∴有24-1个。故答案为:15。
和2都以整体出现,∴有24个集合∵集合为非空集合,∴有24-1个。故答案为:15。
考点:本题考查元素与集合关系的判断。
点评:本题关键看清楚-1和1本身也具备这种运算,这样由-1,1,3和 ,2和
,2和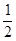 四“大”元素组成集合。
四“大”元素组成集合。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
定义平面向量之间的一种运算“⊙”如下:对任意的
=(m,n),
=(p,q),令
⊙
=mq-np,下面说法错误的是( )
| a |
| b |
| a |
| b |
A、若
| ||||||||||||
B、
| ||||||||||||
C、对任意的λ∈R,有(λ
| ||||||||||||
D、(
|