题目内容
17．y=cosx（x∈[0，π]）与坐标轴所围成的图形的面积是1．分析 根据积分的几何意义，即可求出曲线围成的面积曲线y=cosx（x∈[0，π]）与坐标轴所围成的图形的面积．
解答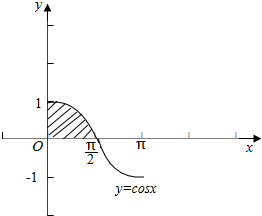 
解：y=cosx（x∈[0，π]）的图象如图，
根据积分的几何意义，y=cosx（x∈[0，π]）与坐标轴所围成的图形的面积
S=${∫}_{0}^{\frac{π}{2}}$cosxdx=sinx${|}_{0}^{\frac{π}{2}}$=sin$\frac{π}{2}$-sin0=1，
故答案为：1．
点评 本题主要考查积分的应用，利用积分即可求出曲线面积，体现了数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
5．设m，n是两条不同的直线，α、β、γ是三个不同的平面，给出下列命题：
①若m⊥α，n∥α，则m⊥n；
②若α∥β，β∥γ，m⊥α，则m⊥γ；
③若m∥α，m∥β，则α∥β；
④若α⊥γ，β⊥γ，则α∥β．
其中正确命题的序号是（ ）
①若m⊥α，n∥α，则m⊥n；
②若α∥β，β∥γ，m⊥α，则m⊥γ；
③若m∥α，m∥β，则α∥β；
④若α⊥γ，β⊥γ，则α∥β．
其中正确命题的序号是（ ）
| A． | ①② | B． | ②③ | C． | ③④ | D． | ①④ |
12．若极坐标方程ρ=ρ（θ）满足ρ（θ）=ρ（π-θ），则方程ρ=ρ（θ）表示的图形关于（ ）
| A． | 极轴对称 | B． | 极点对称 | C． | 射线θ=$\frac{π}{2}$对称 | D． | 不能确定 |
2．演绎推理“因为对数函数y=logax是增函数（大前提），而y=log${\;}_{\frac{1}{3}}$x是对数函数（小前提），所以y=log${\;}_{\frac{1}{3}}$x是增函数（结论）”所得结论错误的原因是（ ）
| A． | 大前提错 | B． | 小前提错 | ||
| C． | 推理形式错 | D． | 大前提和小前提都错 |