题目内容
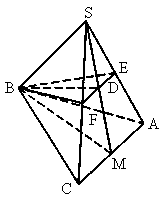
如图,已知正三棱锥S-ABC,过B和侧棱SA、SC的中点E、F作一截面,若这个截面与侧面SAC垂直,求此三棱锥的侧面积与底面积之比.

答案:略
解析:
解析:
|
解:取 AC有中点M,连结SM.设SM∩EF=D.在△ SAC中,E、F分别为SA、SC的中点,∴ EF∥AC.∴  .而SF=FC,∴SD=DM. .而SF=FC,∴SD=DM.
∴ D为SM的中点.∵ S-ABC为正三棱锥,∴△SAC为等腰三角形.∴ SM⊥AC.而AC∥EF,∴ SM⊥EF.又截面BEF⊥侧面SAC.∴ SM⊥平面BEF.∴ SM⊥BD.又SD=DM.∴△ SBM为等腰三角形,∴SB=BM.设正三棱锥 S-ABC的底面边长为a,则 , ,
从而 SA=SB=SC=BM= . .
又  , ,
∴ 
∴  . .
通过截面与侧面垂直,寻找斜高与底面边长的关系,找出二者的关系后,问题就可解决. |

练习册系列答案
相关题目
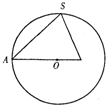 已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为
已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如右图,则此三棱锥的侧面积为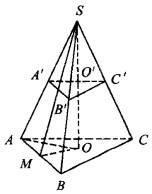 v
v