题目内容
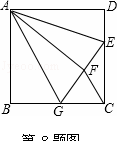
正方形ABCD,沿对角线BD折成直二面角后不会成立的结论是( )
分析:根据已知中正方形ABCD沿对角线BD折成直二面角,我们以O点为坐标原点建立空间坐标系,求出ABCD各点坐标后,进而可以求出相关直线的方向向量及平面的法向量,然后代入线线夹角,线面夹角公式,及模长公式,分别计算即可得到答案.
解答:解:连接AC与BD交于O点,对折后如图所示,令OC=1
则O(0,0,0),A(1,0,0),B(0,1,0),
C(0,0,1),D(0,-1,0)
则
=(-1,0,1),
=(0,-2,0),
∵
•
=0,∴AC⊥BD,故A正确;
∵|
|=|
|=|
|=2,∴△ADC为等边三角形,故B正确;
∵
=(-1,1,0),
=(0,-1,-1),
∴|cos<
,
>|=|
|=
,∴AB与CD所成角为60°,故C正确;
∵
为平面BCD的一个法向量,根据正方形的性质,得AB与平面BCD所成角为45°,故D错误.
故选D.

则O(0,0,0),A(1,0,0),B(0,1,0),
C(0,0,1),D(0,-1,0)
则
| AC |
| BD |
∵
| AC |
| BD |
∵|
| AC |
| AD |
| CD |
∵
| AB |
| CD |
∴|cos<
| AB |
| CD |
| -1 | ||||
|
| 1 |
| 2 |
∵
| OA |
故选D.
点评:本题以平面图形的翻折为载体,考查空间中直线与平面之间的位置关系,根据已知条件构造空间坐标系,将空间线线夹角,线面夹角转化为向量的夹角问题是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目