题目内容
已知函数 +bx(a>0)且f′(1)=0,
+bx(a>0)且f′(1)=0,(1)试用含a的式子表示b,并求函数f(x)的单调区间;
(2)已知A(x1,y1),B(x2,y2)(0<x1<x2)为函数f(x)图象上不同两点,G(x,y)为AB的中点,记AB两点连线斜率为K,证明:f′(x)≠K.
【答案】分析:(1)根据对数函数的定义求得函数的定义域,根据f(x)的解析式求出f(x)的导函数,利用f′(1)=0,代入导函数化简即可得到a与b的关系式,用a表示出b;然后分别令导函数大于0和小于0得到关于x的不等式,求出不等式的解集即可得到相应的x的范围即分别为函数的递增和递减区间;
(2)因为A与B在函数图象上,所以把A和B的坐标分别代入函数解析式中得到关于两点纵坐标的两个关系式,利用斜率的算法表示出斜率k,然后利用中点坐标公式根据A和B的横坐标表示出中点G的横坐标,并把求出的G横坐标的值代入导函数,利用反证法证明,方法是:假设表示出的斜率k等于G的横坐标在导函数的函数值,化简后令t= ,u(t)=lnt-
,u(t)=lnt- ,求出u(t)的导函数,判断出导函数大于0得到u(t)为增函数,得到u(t)小于0与题意矛盾,所以假设错误,故f′(x)≠k.
,求出u(t)的导函数,判断出导函数大于0得到u(t)为增函数,得到u(t)小于0与题意矛盾,所以假设错误,故f′(x)≠k.
解答:解:(1)f(x)的定义域为(0,+∞),
∵f′(x)= ,
,
∴b=a-1,∴f′(x)= ,
,
当f′(x)>0时,得- ,
,
∵x>0,a>0,解得0<x<1,
当f′(x)<0时,得- ,∵x>0,a>0,解得x>1,
,∵x>0,a>0,解得x>1,
;∴当f(x)在(0,1)上单调递增,在(1,+∞)上单调递减;
(2)因A、B在 的图象上,
的图象上,
∴ ,
,
∴ ,
,
∵ ,
,
∴ ,
,
假设k=f′(x),则得: ,
,
即 ,
,
即 ,令
,令 ,
,
∵ ,
,
∴u(t)在(0,1)上是增函数,∴u(t)<u(1)=0,
∴ ,所以假设k=f′(x)不成立,
,所以假设k=f′(x)不成立,
故f′(x)≠k.
点评:此题考查学生会利用导函数的正负求出函数的单调区间,灵活运用中点坐标公式化简求值,掌握反证法进行命题证明的方法,是一道综合题.
(2)因为A与B在函数图象上,所以把A和B的坐标分别代入函数解析式中得到关于两点纵坐标的两个关系式,利用斜率的算法表示出斜率k,然后利用中点坐标公式根据A和B的横坐标表示出中点G的横坐标,并把求出的G横坐标的值代入导函数,利用反证法证明,方法是:假设表示出的斜率k等于G的横坐标在导函数的函数值,化简后令t=
 ,u(t)=lnt-
,u(t)=lnt- ,求出u(t)的导函数,判断出导函数大于0得到u(t)为增函数,得到u(t)小于0与题意矛盾,所以假设错误,故f′(x)≠k.
,求出u(t)的导函数,判断出导函数大于0得到u(t)为增函数,得到u(t)小于0与题意矛盾,所以假设错误,故f′(x)≠k.解答:解:(1)f(x)的定义域为(0,+∞),
∵f′(x)=
 ,
,∴b=a-1,∴f′(x)=
 ,
,当f′(x)>0时,得-
 ,
,∵x>0,a>0,解得0<x<1,
当f′(x)<0时,得-
 ,∵x>0,a>0,解得x>1,
,∵x>0,a>0,解得x>1,;∴当f(x)在(0,1)上单调递增,在(1,+∞)上单调递减;
(2)因A、B在
 的图象上,
的图象上,∴
 ,
,∴
 ,
,∵
 ,
,∴
 ,
,假设k=f′(x),则得:
 ,
,即
 ,
,即
 ,令
,令 ,
,∵
 ,
,∴u(t)在(0,1)上是增函数,∴u(t)<u(1)=0,
∴
 ,所以假设k=f′(x)不成立,
,所以假设k=f′(x)不成立,故f′(x)≠k.
点评:此题考查学生会利用导函数的正负求出函数的单调区间,灵活运用中点坐标公式化简求值,掌握反证法进行命题证明的方法,是一道综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
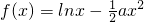 +bx(a>0)且f′(1)=0,
+bx(a>0)且f′(1)=0,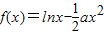 +bx(a>0)且f′(1)=0,
+bx(a>0)且f′(1)=0,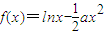 +bx(a>0)且f′(1)=0,
+bx(a>0)且f′(1)=0,