题目内容
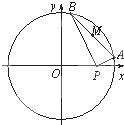 如图所示,已知P(4,0)是圆x2+y2=36内的一点,A,B是圆上两动点,且满足∠APB=90°,求AB的中点M的轨迹方程.
如图所示,已知P(4,0)是圆x2+y2=36内的一点,A,B是圆上两动点,且满足∠APB=90°,求AB的中点M的轨迹方程.分析:设M的坐标为(x,y),连结OM、OA、PA.由垂径定理和直角三角形中线的性质,化简得|AM|2=|PM|2=|OA|2-|OM|2,利用两点的距离公式代入数据,化简即得M的轨迹方程.
解答:解:设M的坐标为(x,y),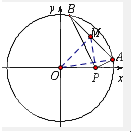 连结OM、OA、PA,
连结OM、OA、PA,
∵在Rt△PAB中,M是斜边AB的中点,∴|PM|=|AM|,
∵由垂径定理,OM⊥AB,
∴|AM|2=|OA|2-|OM|2,可得|PM|2=|OA|2-|OM|2,
可得(x-4)2+y2=36-(x2+y2).
化简得x2+y2-4x-10=0,即为所求AB的中点M的轨迹方程.
 连结OM、OA、PA,
连结OM、OA、PA,∵在Rt△PAB中,M是斜边AB的中点,∴|PM|=|AM|,
∵由垂径定理,OM⊥AB,
∴|AM|2=|OA|2-|OM|2,可得|PM|2=|OA|2-|OM|2,
可得(x-4)2+y2=36-(x2+y2).
化简得x2+y2-4x-10=0,即为所求AB的中点M的轨迹方程.
点评:本题给出动点满足的条件,求动点的轨迹方程.着重考查了圆的方程、两点间的距离公式、垂径定理和直角三角形的性质等知识,属于中档题.

练习册系列答案
相关题目
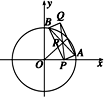
 如图所示,已知P(4,0)是圆x2+y2=36内的一点,A、B是圆上两动点,且满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程.
如图所示,已知P(4,0)是圆x2+y2=36内的一点,A、B是圆上两动点,且满足∠APB=90°,求矩形APBQ的顶点Q的轨迹方程.