题目内容
4.已知三棱锥P-ABC的四个顶点均在同一球面上,其中△ABC为等边三角形,PA⊥平面ABC,PA=2AB=2a,则该球的体积是( )| A. | $\frac{\sqrt{2}}{27}$πa2 | B. | $\frac{32\sqrt{2}}{27}$πa2 | C. | $\frac{32\sqrt{3}}{27}$πa3 | D. | $\frac{32\sqrt{3}}{9}$πa3 |
分析 由题意把三棱锥P-ABC扩展为三棱柱,求出上下底面中心连线的中点与A的距离为球的半径,然后求出球的体积.
解答  解:由题意画出几何体的图形如图,
解:由题意画出几何体的图形如图,
把三棱锥P-ABC扩展为三棱柱,上下底面中心连线的中点与A的距离为球的半径,
PA=2AB=2a,OE=a,△ABC是正三角形,∴AB=a,
∴AE=$\frac{2}{3}\sqrt{{a}^{2}-(\frac{a}{2})^{2}}$=$\frac{\sqrt{3}}{3}$a,
∴AO=$\sqrt{A{E}^{2}+O{E}^{2}}$=$\frac{2\sqrt{3}}{3}$a,
∴V球=$\frac{4}{3}$π•$(\frac{2\sqrt{3}}{3})^{3}$=$\frac{32\sqrt{3}}{27}$πa3,
故选:C.
点评 本题考查球的内接体与球的关系,考查空间想象能力,利用割补法结合球内接多面体的几何特征求出球的半径是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
9.已知等比数列{an}的首项为1,公比为q,前n项和为S,由原数列各项的倒数组成一个新数列{$\frac{1}{{a}_{n}}$},则数列{$\frac{1}{{a}_{n}}$}的前n项和是( )
| A. | $\frac{1}{S}$ | B. | $\frac{1}{{q}^{n}S}$ | C. | $\frac{S}{{q}^{n-1}}$ | D. | $\frac{{q}^{n}}{S}$ |
16.对归纳推理的表述不正确的一项是( )
| A. | 归纳推理是由部分到整体的推理 | |
| B. | 归纳推理是由个别到一般的推理 | |
| C. | 归纳推理是从研究对象的全体中抽取部分进行观察实验,以取得信息,从而对整体做出判断的一种推理 | |
| D. | 归纳推理是由一般到特殊的推理 |
13.已知θ∈(-$\frac{π}{2}$,0)且3tanθ•sinθ=8,则cos($\frac{3π}{2}$-2θ)的值为( )
| A. | -$\frac{4\sqrt{2}}{9}$ | B. | $\frac{4\sqrt{2}}{9}$ | C. | -$\frac{2\sqrt{2}}{9}$ | D. | $\frac{2\sqrt{2}}{9}$ |
 为两个朝下的面上的数字之和.
为两个朝下的面上的数字之和. 不小于6”的概率;
不小于6”的概率; 为奇数”的概率和“
为奇数”的概率和“ 为偶数”的概率是不是相等?证明你作出的结论.
为偶数”的概率是不是相等?证明你作出的结论.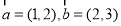 ,若向量
,若向量 与向量
与向量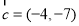 共线,则
共线,则 .
.