题目内容
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,则下列结论正确的是( )

A.PB⊥AD
B.平面PAB⊥平面PBC
C.直线BC∥平面PAE
D.直线EF∥平面PAD
D
解析:
因为AD与PB在平面ABC内的射影AB不垂直,所以A答案不正确;过点A作PB的垂线,垂足为H,若平面PAB⊥平面PBC,则AH⊥平面PBC,所以AH⊥BC,又PA⊥BC,所以BC⊥平面PAB,则BC⊥AB,这与底面是正六边形不符,所以B答案不正确;若直线BC∥平面PAE,则BC∥AE,但BC与AE相交,所以C答案不正确。

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目

 16、如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中:
16、如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中: 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD与平面PAB所成角的余弦值为
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD与平面PAB所成角的余弦值为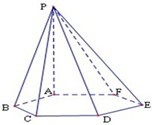 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论不正确的序号是
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则下列结论不正确的序号是