题目内容
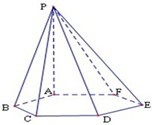如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC．则下列结论不正确的序号是④
④
．①CD∥平面PAF
②DF⊥平面PAF
③CF∥平面PAB
④CF⊥平面PAD．
分析：直接利用棱锥的结构特征，判断选项即可得到结果．
解答：解：因为几何体是六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC．
所以①CD∥平面PAF，CD∥AF，CD?平面PAF，AF?平面PAF，满足直线与平面平行的判定定理，所以CD∥平面PAF，正确．
②DF⊥平面PAF，因为DF⊥AF，PA⊥底面ABCDEF，满足直线与平面垂直的判定定理，正确．
③CF∥平面PAB，CF∥AB，CF?平面PAB，AB?平面PAB，满足直线与平面平行的判定定理，所以CF∥平面PAB，正确．
④CF⊥平面PAD．不满足直线与平面垂直的判定定理，不正确．
故答案为：④．
所以①CD∥平面PAF，CD∥AF，CD?平面PAF，AF?平面PAF，满足直线与平面平行的判定定理，所以CD∥平面PAF，正确．
②DF⊥平面PAF，因为DF⊥AF，PA⊥底面ABCDEF，满足直线与平面垂直的判定定理，正确．
③CF∥平面PAB，CF∥AB，CF?平面PAB，AB?平面PAB，满足直线与平面平行的判定定理，所以CF∥平面PAB，正确．
④CF⊥平面PAD．不满足直线与平面垂直的判定定理，不正确．
故答案为：④．
点评：本题考查棱锥的结构特征，直线与平面平行与垂直的判定定理的应用，考查逻辑推理能力．
练习册系列答案
相关题目
16、如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB，则下列结论中：
如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB，给出下列结论：①PB⊥AE；②平面ABC⊥平面PBC；③直线BC∥平面PAE；④∠PDA=45°；⑤直线PD与平面PAB所成角的余弦值为