题目内容
9、如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB则下列结论正确的是（ ）
分析：利用题中条件，逐一分析答案，通过排除和筛选，得到正确答案．
解答：解：∵AD与PB在平面的射影AB不垂直，
所以A不成立，又，平面PAB⊥平面PAE，
所以平面PAB⊥平面PBC也不成立；BC∥AD∥平面PAD，
∴直线BC∥平面PAE也不成立．
在Rt△PAD中，PA=AD=2AB，∴∠PDA=45°，
故选D．
所以A不成立，又，平面PAB⊥平面PAE，
所以平面PAB⊥平面PBC也不成立；BC∥AD∥平面PAD，
∴直线BC∥平面PAE也不成立．
在Rt△PAD中，PA=AD=2AB，∴∠PDA=45°，
故选D．
点评：本题考查直线与平面成的角、直线与平面垂直的性质．
练习册系列答案
相关题目
16、如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB，则下列结论中：
如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB，给出下列结论：①PB⊥AE；②平面ABC⊥平面PBC；③直线BC∥平面PAE；④∠PDA=45°；⑤直线PD与平面PAB所成角的余弦值为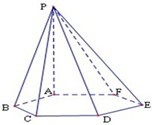
如图，已知六棱锥P-ABCDEF的底面是正六边形，PA⊥平面ABC．则下列结论不正确的序号是