题目内容
已知椭圆及圆的方程分别为| x2 |
| a2 |
| y2 |
| b2 |
分析:先设A(x0,y0),则过A的圆的切线方程为x0x+y0y=r2,将其与椭圆方程联立,得一一元二次方程,由△=0,整理后即可得|AB|=f(r),求f(x)最大值时使用均值定理,注意等号成立的条件.
解答:解:设A(x0,y0),则过A的圆的切线方程为x0x+y0y=r2,代入
+
=1,得
(b2+
)x2-
x+
-a2b2=0
由△=0得(x-x0)2+(y-y0)2=a2+b2-
-x2
∴
∵
+x2≥2
=2ab
∴f(x)≤
=a-b
(当且仅当x=
时取等号)
∴
f(x)的最大值为a-b
| x2 |
| a2 |
| y2 |
| b2 |
(b2+
| a2 x02 |
| y02 |
| 2a2r2x0 |
| y02 |
| a2r4 |
| y02 |
由△=0得(x-x0)2+(y-y0)2=a2+b2-
| a2b2 |
| r2 |
∴
|
∵
| a2b2 |
| x2 |
|
∴f(x)≤
| a2+b2-2ab |
(当且仅当x=
| ab |
∴
|
f(x)的最大值为a-b
点评:本题考查了圆与椭圆的关系,直线与曲线相切的关系,有一定的运算量,解题时要耐心细致

练习册系列答案
相关题目
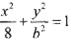 ,F1、F2分别是椭圆C的左、右焦点,离心率e=
,F1、F2分别是椭圆C的左、右焦点,离心率e= .
.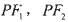 都与以Q为圆心的一个圆相切,如存在,求出P点坐标及圆的方程,如不存在,请说明理由.
都与以Q为圆心的一个圆相切,如存在,求出P点坐标及圆的方程,如不存在,请说明理由.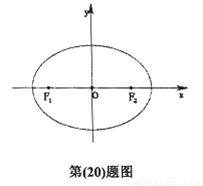
 与椭圆交于A,B两点,
与椭圆交于A,B两点, 的面积为4,
的面积为4, 的周长为
的周长为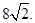 (I)求椭圆C的方程;(II)设点Q的坐标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。
(I)求椭圆C的方程;(II)设点Q的坐标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。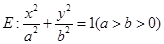 过点
过点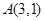 ,左、右焦点分别为
,左、右焦点分别为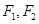 ,离心率为
,离心率为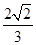 ,经过
,经过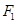 的直线
的直线 与圆心在
与圆心在 轴上且经过点
轴上且经过点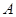 的圆
的圆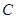 恰好相切于点
恰好相切于点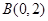 .
.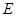 及圆
及圆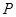 ,使
,使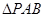 为以
为以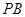 为底边的等腰三角形?若存在,求点
为底边的等腰三角形?若存在,求点 过点
过点 ,左、右焦点分别为
,左、右焦点分别为 ,离心率为
,离心率为 ,经过
,经过 的直线
的直线 与圆心在
与圆心在 轴上且经过点
轴上且经过点 的圆
的圆 恰好相切于点
恰好相切于点 .
. 及圆
及圆 ,使
,使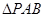 为以
为以 为底边的等腰三角形?若存在,求点
为底边的等腰三角形?若存在,求点