题目内容
(本小题满分12分)
已知椭圆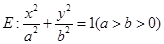 过点
过点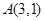 ,左、右焦点分别为
,左、右焦点分别为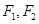 ,离心率为
,离心率为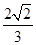 ,经过
,经过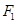 的直线
的直线 与圆心在
与圆心在 轴上且经过点
轴上且经过点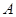 的圆
的圆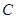 恰好相切于点
恰好相切于点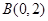 .
.
(1)求椭圆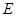 及圆
及圆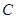 的方程;
的方程;
(2) 在直线 上是否存在一点
上是否存在一点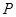 ,使
,使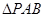 为以
为以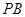 为底边的等腰三角形?若存在,求点
为底边的等腰三角形?若存在,求点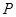 的坐标,否则说明理由.
的坐标,否则说明理由.
【答案】
解:(1)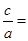
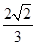 ,则
,则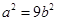 ,
,
∴椭圆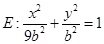 ,
,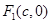 ,
,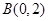
∴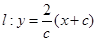 …………3分
…………3分
设圆心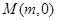 ,半径
,半径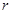 ,则由
,则由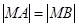 ,得
,得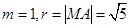
∴圆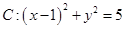 ,又
,又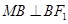
∴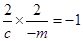 ,从而
,从而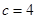 ,结合
,结合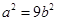 得
得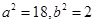
∴椭圆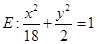 ………………………6分
………………………6分
(2)假设存在一点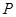 ,使
,使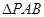 为以
为以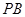 为底边的等腰三角形,则有
为底边的等腰三角形,则有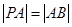 ,
,
由(1)知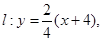 即
即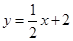 ,设直线
,设直线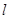 上的点
上的点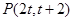 ,
,
∴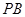 中点
中点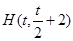 ,又
,又 ,
,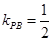 ,
,
由 得
得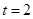
∴所求的点为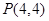 ……………………………12分
……………………………12分
【解析】略

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目