题目内容
已知数列{an}的首项是a1=1,前n项和为Sn,且Sn+1=2Sn+3n+1(n∈N*).(1)设bn=an+3(n∈N*),求数列{bn}的通项公式;
(2)设cn=log2bn,若存在常数k,使不等式
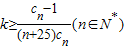 恒成立,求k的最小值.
恒成立,求k的最小值.
【答案】分析:(1))∵Sn+1=2Sn+3n+1,∴当n≥2时,Sn=2Sn-1+3(n-1)+1,两式相减得an+1=2an+3,从而bn+1=an+1+3=2(an+3)=2bn(n≥2),由此可以导出数列{bn}的通项公式.
(2)由题意知cn=log2bn=log24×2n-1=log22n+1,再用均值不等式进行求解.
解答:解:(1)∵Sn+1=2Sn+3n+1,
∴当n≥2时,Sn=2Sn-1+3(n-1)+1,两式相减得an+1=2an+3,从而bn+1=an+1+3=2(an+3)=2bn(n≥2),
∵S2=2S1+3+1,
∴a2=a1+4=5,可知b2≠0.
∴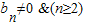 .
.
∴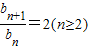 ,又
,又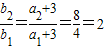 .
.
∴数列{bn}是公比为2,首项为4的等比数列,
因此bn=4•2n-1=2n+1(n∈N*)
(2)据(1)cn=log2bn=log24×2n-1=log22n+1=n+1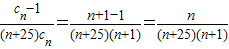 =
=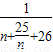
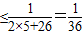 ,(当且仅当n=5时取等号).
,(当且仅当n=5时取等号).
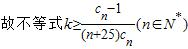 恒成立,
恒成立,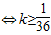 .
.
点评:本题考查数列的综合运用,解题时要注意均值不等式的合理运用.
(2)由题意知cn=log2bn=log24×2n-1=log22n+1,再用均值不等式进行求解.
解答:解:(1)∵Sn+1=2Sn+3n+1,
∴当n≥2时,Sn=2Sn-1+3(n-1)+1,两式相减得an+1=2an+3,从而bn+1=an+1+3=2(an+3)=2bn(n≥2),
∵S2=2S1+3+1,
∴a2=a1+4=5,可知b2≠0.
∴
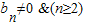 .
.∴
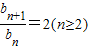 ,又
,又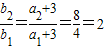 .
.∴数列{bn}是公比为2,首项为4的等比数列,
因此bn=4•2n-1=2n+1(n∈N*)
(2)据(1)cn=log2bn=log24×2n-1=log22n+1=n+1
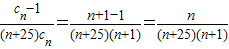 =
=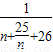
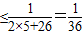 ,(当且仅当n=5时取等号).
,(当且仅当n=5时取等号).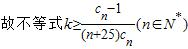 恒成立,
恒成立,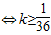 .
.点评:本题考查数列的综合运用,解题时要注意均值不等式的合理运用.

练习册系列答案
相关题目