题目内容
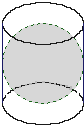 如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现:
如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现:(1)求圆柱的体积与球的体积之比;
(2)求圆柱的表面积与球的表面积之比.
分析:(1)设圆柱的高为h,底面半径为r,球的半径为R,求出圆柱的体积,球的体积,即可得到结论.
(2)求出圆柱的表面积,球的表面积即可得到比值.
(2)求出圆柱的表面积,球的表面积即可得到比值.
解答:解:(1)设圆柱的高为h,底面半径为r,球的半径为R,由已知得h=2R,r=R.
∵V圆柱=πR2•2R.
∴
=
=
.
(2)∵S圆柱=S侧+2S底=2πrh+2πr2=6πr2,S球=4πr2.
∴
=
=
.
∵V圆柱=πR2•2R.
∴
| V圆柱 |
| V球 |
| 2πR3 | ||
|
| 3 |
| 2 |
(2)∵S圆柱=S侧+2S底=2πrh+2πr2=6πr2,S球=4πr2.
∴
| S圆柱 |
| S球 |
| 6πr2 |
| 4πr2 |
| 3 |
| 2 |
点评:本题是基础题,看错圆柱和球的体积、表面积,考查计算能力,常考题目.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现.圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为( )
如图所示是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形表达了阿基米德最引以为自豪的发现.我们来重温这个伟大发现.圆柱的体积与球的体积之比和圆柱的表面积与球的表面积之比分别为( )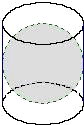 如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现:
如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现: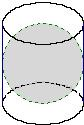
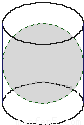 如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现:
如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现: