题目内容
已知三棱锥S-ABC的所有顶点都在球O的球面上,SC为球O的直径,且SC⊥OA,SC⊥OB,△OAB为等边三角形,三棱锥S-ABC的体积为
,则球O的半径为( )
4
| ||
| 3 |
分析:根据题意作出图形,欲求球的半径r.利用截面的性质即可得到三棱锥S-ABC的体积可看成是两个小三棱锥S-ABO和C-ABO的体积和,即可计算出三棱锥的体积,从而建立关于r的方程,即可求出r,从而解决问题.
解答: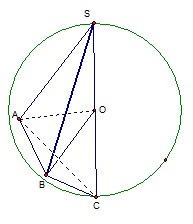 解:根据题意作出图形:
解:根据题意作出图形:
设球心为O,球的半径r.
∵SC⊥OA,SC⊥OB,∴SC⊥平面AOB,
三棱锥S-ABC的体积可看成是两个小三棱锥S-ABO和C-ABO的体积和.
∴V三棱锥S-ABC=V三棱锥S-ABO+V三棱锥C-ABO=
×
×r2×r×2=
,
∴r=2.
故选C.
 解:根据题意作出图形:
解:根据题意作出图形:设球心为O,球的半径r.
∵SC⊥OA,SC⊥OB,∴SC⊥平面AOB,
三棱锥S-ABC的体积可看成是两个小三棱锥S-ABO和C-ABO的体积和.
∴V三棱锥S-ABC=V三棱锥S-ABO+V三棱锥C-ABO=
| 1 |
| 3 |
| ||
| 4 |
4
| ||
| 3 |
∴r=2.
故选C.
点评:本题考查棱锥的体积,考查球内接多面体,解题的关键是确定点三棱锥S-ABC的体积可看成是两个小三棱锥S-ABO和C-ABO的体积和.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目