题目内容
设z=kx+y,其中实数x,y满足 若z的最大值为12,则实数k= .
若z的最大值为12,则实数k= .
 若z的最大值为12,则实数k= .
若z的最大值为12,则实数k= .2
作出可行域(如图),其中A(4,4),B(0,2),C(2,0)
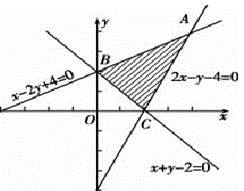
过原点作出直线kx+y=0
② k=0时,y=0,目标函数z=y在点A处取得最大值4,与题意不符
②
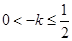 即
即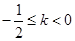 时,直线kx+y=0即y=-kx经过一、三象限,平移直线y=-kx可知,目标函数z=kx+y在点A处取得最大值,即
时,直线kx+y=0即y=-kx经过一、三象限,平移直线y=-kx可知,目标函数z=kx+y在点A处取得最大值,即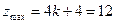 ,此时k=2与
,此时k=2与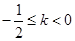 不符;
不符;③-k>
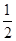 即k<-
即k<-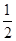 时,直线kx+y=0即y=-kx经过一、三象限,平移直线y=-kx可知,目标函数z=kx+y在点B处取得最大值,即
时,直线kx+y=0即y=-kx经过一、三象限,平移直线y=-kx可知,目标函数z=kx+y在点B处取得最大值,即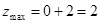 ,此式不成立
,此式不成立④-k<0即k>0时,直线kx+y=0即y=-kx经过二、四象限,平移直线y=-kx可知,目标函数z=kx+y在点A处取得最大值,即
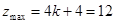 ,此时k=2与k>0相符,所以k=2
,此时k=2与k>0相符,所以k=2
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足约束条件
满足约束条件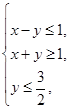 若
若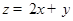 的最大值是 .
的最大值是 .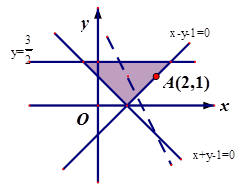
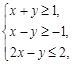 目标函数z=ax+2y仅在点(1,0)处取得最小值,则实数a的取值范围是( )
目标函数z=ax+2y仅在点(1,0)处取得最小值,则实数a的取值范围是( )

 给定. 若
给定. 若 为D上的动点,点A的坐标为
为D上的动点,点A的坐标为 ,则
,则 的最大值为( )
的最大值为( )

 所表示的平面区域被直线
所表示的平面区域被直线 分成面积相等的两
分成面积相等的两 所表示的区域上一动点,则直线OM斜率的最小值为( )
所表示的区域上一动点,则直线OM斜率的最小值为( )

 、
、 满足不等式组
满足不等式组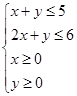 ,则
,则 的最大值是____________.
的最大值是____________. 是不等式组
是不等式组 所表示的平面区域内任意一点,则点M到直线
所表示的平面区域内任意一点,则点M到直线 距离的最大值为( )
距离的最大值为( )


 满足约束条件
满足约束条件 则
则 的取值范围是_________.
的取值范围是_________.