题目内容
【题目】已知函数![]() (k为常数,
(k为常数,![]() 且
且![]() ).
).
(1)在下列条件中选择一个________使数列![]() 是等比数列,说明理由;
是等比数列,说明理由;
①数列![]() 是首项为2,公比为2的等比数列;
是首项为2,公比为2的等比数列;
②数列![]() 是首项为4,公差为2的等差数列;
是首项为4,公差为2的等差数列;
③数列![]() 是首项为2,公差为2的等差数列的前n项和构成的数列.
是首项为2,公差为2的等差数列的前n项和构成的数列.
(2)在(1)的条件下,当![]() 时,设
时,设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
【答案】(1)②,理由见解析;(2)![]()
【解析】
(1)选②,由![]() 和对数的运算性质,以及等比数列的定义,即可得到结论;
和对数的运算性质,以及等比数列的定义,即可得到结论;
(2)运用等比数列的通项公式可得![]() ,进而得到
,进而得到![]() ,由数列的裂项相消求和可得所求和.
,由数列的裂项相消求和可得所求和.
(1)①③不能使![]() 成等比数列.②可以:由题意
成等比数列.②可以:由题意![]() ,
,
即![]() ,得
,得![]() ,且
,且![]() ,
,![]() .
.
![]() 常数
常数![]() 且
且![]() ,
,![]() 为非零常数,
为非零常数,
![]() 数列
数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
(2)由(1)知![]() ,所以当
,所以当![]() 时,
时,![]() .
.
因为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
![]()
![]() .
.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
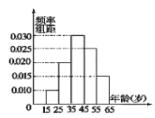
【题目】为了宣传今年10月在某市举行的“第十届中国艺术节”,“十艺节”筹委会举办了“十艺节”知识有奖问答活动,随机对市民15~65岁的人群抽样![]() 人,回答问题统计结果如下图表所示:
人,回答问题统计结果如下图表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | 频率分布直方图 |
第1组 |
| 5 | 0.5 |
|
第2组 |
|
| 0.9 | |
第3组 |
| 27 |
| |
第4组 |
| 9 | 0.36 | |
第5组 |
| 3 | 0.2 |
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,“十艺节”筹委会决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.