题目内容
3．某种型号的汽车，如果速度在100千米/小时以内时，在高速公路上它的刹车距离s（米）与汽车的车速x（千米/小时）有如下关系：s=0.005x2+0.1x（x＜100）．在某次交通事故中，测得肇事汽车刹车距离大于40米，问这辆汽车的车速至少为每小时多少千米？分析 由题意可得0.005x2+0.1x＞40，解关于x的不等式可得．
解答 解：由题意可得0.005x2+0.1x＞40，
整理可得x2+20x-8000＞0，
分解因式可得（x-20）（x+40）＞0，
解得x＜-40或x＞20，
结合x＜100可得20＜x＜100
故汽车的车速至少为每小时20千米．
点评 本题考查不等式的解法，属基础题．
练习册系列答案
相关题目
14．已知{an}是公比小于1的等比数列，且a2=2，a1+a3=5，设Tn=a1a2+a2a3+a3a4+…+anan+1，则（ ）
| A． | 12≤Tn＜16 | B． | 8≤Tn＜16 | C． | 12≤Tn＜$\frac{32}{3}$ | D． | 8≤Tn＜$\frac{32}{3}$ |
11．
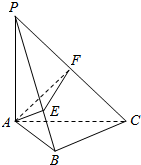《九章算术》中，将四个面都为直角三角形的四面体称之为鳖臑，如图，在鳖臑PABC中，PA⊥平面ABC，AB⊥BC，且AP=AC=1，过A点分别作AE⊥PB于E、AF⊥PC于F，连接EF当△AEF的面积最大时，tan∠BPC的值是（ ）
《九章算术》中，将四个面都为直角三角形的四面体称之为鳖臑，如图，在鳖臑PABC中，PA⊥平面ABC，AB⊥BC，且AP=AC=1，过A点分别作AE⊥PB于E、AF⊥PC于F，连接EF当△AEF的面积最大时，tan∠BPC的值是（ ）| A． | $\sqrt{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\sqrt{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
18．设函数f（x）=$\left\{\begin{array}{l}{x+\frac{1}{x+1}-\frac{1}{2}，x≥1}\\{1，x＜1}\end{array}\right.$，则不等式f（6-x2）＞f（x）的解集为（ ）
| A． | （-3，1） | B． | （-3，2） | C． | （-2，$\sqrt{5}$） | D． | （-$\sqrt{5}$，2） |