题目内容
8.已知函数f(x)=$\frac{lnx+k}{x}$在(0,+∞)存在最大值,且最大值为1.(1)求实数k的值;
(2)若不等式f′(x)>$\frac{1}{4}$a-$\frac{2a+1}{2x}$在(0,2]恒成立,求实数a的取值范围.
分析 (1)求导f′(x)=$\frac{-lnx-k+1}{{x}^{2}}$,从而由导数的正负确定函数的单调性,从而求最大值并令其为1,从而解得;
(2)化简原不等式可得2lnx+$\frac{1}{2}$ax2-(2a+1)x<0,记g(x)=2lnx+$\frac{1}{2}$ax2-(2a+1)x,求导g′(x)=$\frac{(ax-1)(x-2)}{x}$,从而分类讨论以确定函数的单调性,从而化恒成立问题为最值问题即可.
解答 解:(1)∵f(x)=$\frac{lnx+k}{x}$,
∴f′(x)=$\frac{-lnx-k+1}{{x}^{2}}$,
由f′(x)=0得x=e1-k,
当x∈(0,e1-k)时,f(x)单调递增,当x∈(e1-k,+∞)时,f(x)单调递减,
故f(x)的最大值为f(e1-k)=ek-1=1,所以k=1;
(2)原不等式可变形为2lnx+$\frac{1}{2}$ax2-(2a+1)x<0,
记g(x)=2lnx+$\frac{1}{2}$ax2-(2a+1)x,g′(x)=$\frac{(ax-1)(x-2)}{x}$,
当a≤0时,g′(x)≥0,即g(x)在(0,2]递增,
所以gmin(x)=g(2)=2ln2-2a-2<0,
解得a>ln2-1,故ln2-1<a≤0;
当0<a≤$\frac{1}{2}$时,g′(x)≥0,g(x)在(0,2]递增,
所以gmin(x)=g(2)=2ln2-2a-2<0,
解得a>ln2-1,故0<a≤$\frac{1}{2}$;
当a>$\frac{1}{2}$时,由g′(x)<0得$\frac{1}{a}$<x≤2,由g′(x)>0得0<x<$\frac{1}{a}$;
所以g(x)在(0,$\frac{1}{a}$)递增,在($\frac{1}{a}$,2)递减,
故gmin(x)=g($\frac{1}{a}$)=-2lna-$\frac{1}{2a}$-2<0,
记h(a)=-2lna-$\frac{1}{2a}$-2(a>$\frac{1}{2}$),则h′(a)=$\frac{1-4a}{2{a}^{2}}$<0,
h(a)<h($\frac{1}{2}$)=2ln2-3<0,故a>$\frac{1}{2}$;
综上所述,实数a的取值范围是a>ln2-1.
点评 本题考查了导数的综合应用及恒成立问题的处理方法应用,同时考查了分类讨论的思想应用.

| A. | 最大值是f(1),最小值是f(3) | B. | 最大值是f(3),最小值是f(1) | ||
| C. | 最大值是f(1),最小值是f(2) | D. | 最大值是f(2),最小值是f(3) |
| A. | ?x0∈R,使得${e^{x_0}}≤0$ | B. | ?x∈R,x2+1<3x | ||
| C. | ?x0∈R,使得|x0-3|+|x0-1|<2 | D. | ?x>0,x+$\frac{4}{x}$≥4 |
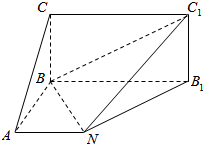 如图,矩形BB1C1C所在平面与底面ANB1B垂直,在直角梯形ANB1B中,AB⊥AN,CB=BA=AN=4,BB1=8,AN∥BB1.
如图,矩形BB1C1C所在平面与底面ANB1B垂直,在直角梯形ANB1B中,AB⊥AN,CB=BA=AN=4,BB1=8,AN∥BB1.