Question

（2009•河东区二模）已知一个正四棱锥的底面是一个棱长为1的正方体的某个面，且这个正四棱锥与正方体有相同的全面积，则这个正四棱锥的侧棱与底面所成角的余弦值为

13

13

．

Answer 1

分析：由题意可得买这个正四棱锥的全面积为6，设这个正四棱锥的斜高为h，则1+4×（

1

2

×1×h）=6，解得h的值，可得侧棱长为PC=

h2+( 1 2 )2

的值．再根据侧棱与底面所成角的余弦值为 cosθ=

OC

PC

，运算求得结果．

解答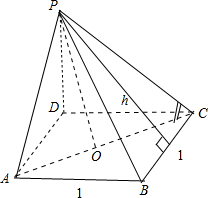：解：由题意可得买这个正四棱锥的全面积为6，如图所示，PO⊥平面ABCD．
设这个正四棱锥的斜高为h，则1+4×（

1

2

×1×h）=6，解得 h=

5

2

，
∴侧棱长为PC=

h2+( 1 2 )2

=

26

2

，
这个正四棱锥 的侧棱与底面所成角的余弦值为 cosθ=

OC

PC

=

2 2

26 2

=

13

13

，
故答案为

13

13

．

点评：本题主要考查直线和平面所成的角的定义和求法，直角三角形中的边角关系，属于中档题．